Section 4 Problem Set 4
- Due: Tuesday June 15 by midnight CST.
- Upload your solutions to Moodle in a PDF.
- Please feel free to use RStudio for all row reductions.
- You can download the Rmd source file for this problem set.
The Problem Set covers sections 2.2-2.3 on Matrix Inverses and 4.1-4.3 on Subspaces and Bases.
4.1 Rainy Day in LA
In Los Angeles if it rains today, there is a 50% chance it will rain tomorrow, but it if is sunny today, there is a 90% chance it will be sunny tomorrow. This is modeled in the rain-sunshine probability matrix P. \[ P = \begin{array}{c|cc|} &\text{rain}&\text{sun}\\ \hline \text{rain}&1/2&1/10\\ \text{sun}&1/2&9/10\\ \hline \end{array} \] This matrix works as follows: if the rain-sunshine probability today is (40, 60) (that is, 40% chance rain and 60% chance sunshine), then the rain-sunshine probability tomorrow is (26, 74) as seen by the calculation below. \[ \begin{bmatrix} 1/2 & 1/10 \\ 1/2 & 9/10 \\ \end{bmatrix} \begin{bmatrix} 40 \\ 60 \end{bmatrix} = \begin{bmatrix} 26 \\ 74 \end{bmatrix} \]
Find the rain-sunshine probability the day after tomorrow.
Compute \(P^2\) and explain the meaning of each of the four entries in the matrix.
Find \(P^{-1}\) and and use it find the rain-sunshine probability yesterday if the rain-sunshine probability today is (40, 60).
4.2 Fibonacci Vectors
The Fibonacci vectors \(F\) in \(\mathbb{R}^5\) are defined below: \[ F = \left\{ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} ~\Bigg\vert~ \ x_3 = x_1 + x_2, x_4 = x_2 + x_3, x_5 = x_3 + x_4 \right\} \subseteq \mathbb{R}^5. \hskip5in \]
Show that \(F\) is a subspace.
Find a basis for \(F\). Show that your vectors span \(F\) and are linearly independent.
4.3 Vectors Rescaled
If the function \(T: \mathbb{R}^n \to \mathbb{R}^n\) is a linear transformation, then show that the set below is a subspace of \(\mathbb{R}^n\) \[ E_{2021} = \{\ \vec{x} \in \mathbb{R}^n \mid T(\vec{x}) = 2021 \vec{x} \}. \] Is there anything special about 2021 in the definition? If it were replaced by another scalar, would it still be a subspace?
4.4 Column and Null Space
Find a basis for the column space \(Col(A)\) and the null space \(Nul(A)\) of the matrix \(A\) below
(A = rbind(c(1, 2, 0, 2, 0, -1),c(1, 2, 1, 1, 0, -2),
c(2, 4, -2, 6, 1, 2),c(1, 2, 0, 2, -1, -3 )))## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 2 0 2 0 -1
## [2,] 1 2 1 1 0 -2
## [3,] 2 4 -2 6 1 2
## [4,] 1 2 0 2 -1 -34.5 Extend to a basis
I am interested in the vectors below. I know that they do not span \(\mathbb{R}^5\), because there are not enough of them, but I want to extend this set to a basis of \(\mathbb{R}^5\) by adding some vectors to the set. \[ \begin{bmatrix} 5\\ 4\\ 3\\ 1\\ 2 \end{bmatrix}, \begin{bmatrix} 4\\ 4\\ 3\\ 1\\ 2 \end{bmatrix}, \begin{bmatrix} 1\\ 1\\ 1\\ 1\\ 1\end{bmatrix}. \] I searched online for ideas and one suggested that I make the matrix below and row reduce it.
(A = cbind(c(5,4,3,1,2),c(4,4,3,1,2),c(1,1,1,1,1),diag(5)))## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 5 4 1 1 0 0 0 0
## [2,] 4 4 1 0 1 0 0 0
## [3,] 3 3 1 0 0 1 0 0
## [4,] 1 1 1 0 0 0 1 0
## [5,] 2 2 1 0 0 0 0 1Row reduce this matrix.
Use the result to come up with a basis for \(\mathbb{R}^5\) that includes my original 3 vectors
Explain why this method works.
4.6 Getting Into a Subspace
Let \(S \subset \mathbb{R}^n\) be a subspace and let \(\mathsf{v}, \mathsf{w} \in \mathbb{R}^n\). For each of the following statements, either give a specific example or explain why it cannot happen.
If \(\mathsf{v}\) is not in \(S\) and \(c\) is a nonzero constant, can \(c\mathsf{v}\) be in \(S\)?
If \(\mathsf{v}\) is not in \(S\) and \(\mathsf{w}\) is not in \(S\), can \(\mathsf{v} + \mathsf{w}\) be in \(S\)?
If \(\mathsf{v}\) is in \(S\) and \(\mathsf{w}\) is not in \(S\) can \(\mathsf{v} + \mathsf{w}\) be in \(S\)?
4.7 A Vector in Both Col(A) and Nul(A)
Give a \(3 \times 3\) matrix \(A\) for which the vector \(\mathsf{v} = \begin{bmatrix}3 \\ -2 \\ 5 \end{bmatrix}\) is in both \(\mathrm{Col}(A)\) and \(\mathrm{Nul}(A)\). Be sure to demonstrate that \(\mathsf{v} \in \mathrm{Col}(A)\) and \(\mathsf{v} \in \mathrm{Nul}(A)\).
4.8 Adjacency Matrix
You can do this problem in R or by hand. Consider the matrix \(A\) defined here
A = rbind(c( 0 , 1 , 0 , 1 , 1 ,0), c(1 , 0 , 1 , 1 , 0, 0 ),c( 0 , 1 , 0 , 1 , 1, 0 ),
c( 1 , 1 , 1 , 0 , 1, 0 ),c( 1 , 0 , 1 , 1 , 0, 1 ), c(0, 0, 0, 0, 1, 0))
A## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0 1 0 1 1 0
## [2,] 1 0 1 1 0 0
## [3,] 0 1 0 1 1 0
## [4,] 1 1 1 0 1 0
## [5,] 1 0 1 1 0 1
## [6,] 0 0 0 0 1 0This matrix represents the connections in the network diagram below. There is a 1 in position \((i,j)\) of the matrix if there is a connection (an edge) between vertex \(i\) and vertex \(j\) and there is a 0 if there is not.
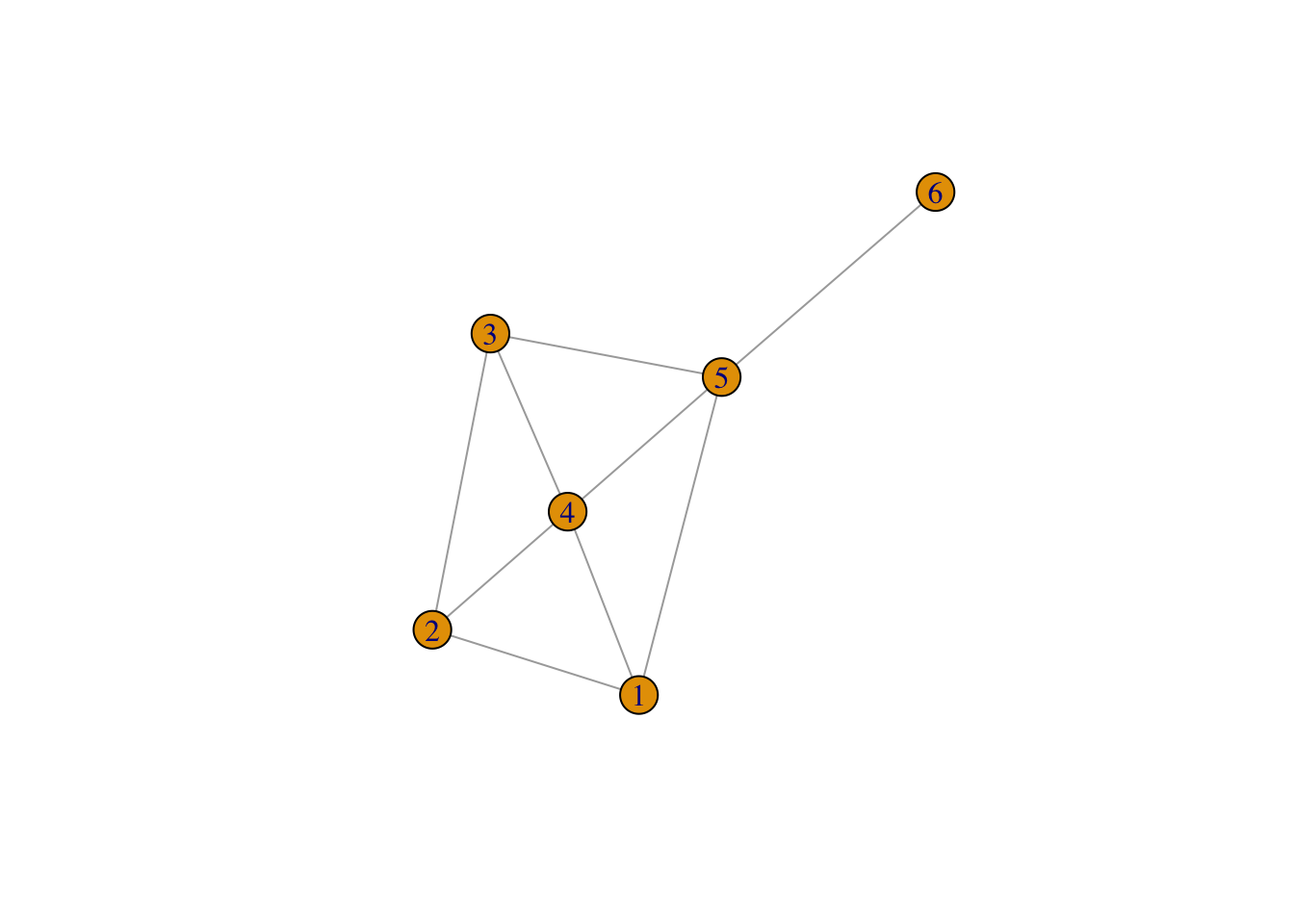
Compute \(A v\) where \(v\) is the vector of all 1’s. Explain what this new vector tells us about the graph.
Compute \(A^2 = A A\), the square of the matrix \(A\).
Look at the \((2,5)\) entry of \(A^2\). Explain what this entry says about connections in the network. Do the same for the \((2,3)\) and the \((2,6)\) entry of \(A^2\).