Section 9 Field Constructions
9.1 Polynomial Rings
Let \(R\) be an integral domain, and consider the ring of polynomials in \(R\) in one variable \[ R[x] = \{ a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n \mid n \ge 0, a_i \in R\} \] The polynomial is a commutative ring with unity equal to the polynomial 1. There are no zero divisors, so \(R[x]\) is an integral domain. We also have \[ R \subseteq R[x] \] as the subring of scalar polynomials. The units in \(R[x]\) are the units in \(R\).
The degree of a polynomial \(p(x) \in R[x]\) is the highest power of \(x\) with a nonzero coefficient. For example,
- \(\deg(3 x^5 + 2 x^3 - 11 x + 10) = 5\)
- \(\deg(7x -4 ) = 1\)
- \(\deg(13) = 0\)
- \(\deg(0) = -\infty\) (or, sometimes, it is said to b undefined).
Observe that \[ (5 x^3 + 2 x - 11)(-2 x^4 + 3 x^3 -2x + 4) = -10 x^7 + 15 x^6 \cdots - 44. \] As we can see, if \(R\) is an integral domain, then \[ \deg(p(x)q(x)) = \deg(p(x))+\deg(q(x)). \]
We are especially interested in the case where \(R = \mathbb{F}\) is a field. In that case we have a division algorithm, which is both an algorithm and a theorem:
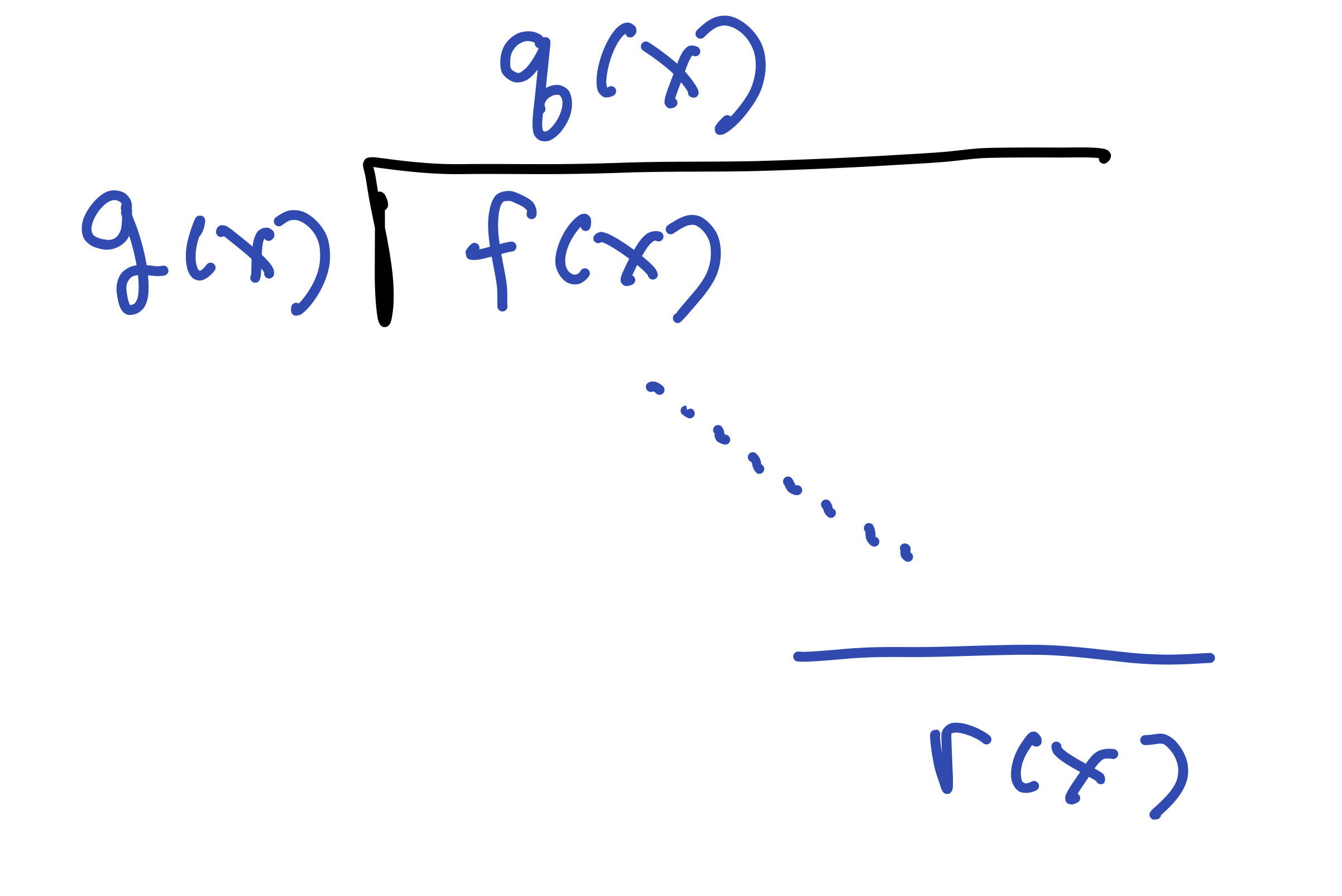
Theorem (Division Algorithm) If \(f(x), g(x) \in \mathbb{F}[x]\) with \(g(x) \not = 0\), then there exist unique polynomials \(q(x),r(x) \in \mathbb{F}[x]\) such that \[ f(x)= g(x) q(x) + r(x), \qquad \hbox{with}\quad \deg(r(x)) < \deg(g(x)). \]
The proof of this is to show that the algorithm for polynomial division that we learned in high school works, arrives at unique quotients and remainders, and ends with a remainder that is smaller than the degree of \(g(x)\). The proof is by induction on the degree of \(f(x)\).
 Theorem (Remainder Theorem) If \(a \in \mathbb{F}\) and \(f(x) \in \mathbb{F}[x]\) then \(f(a)\) is the remainder after division of \(f(x)\) by \((x-a)\). That is,
\[
f(x) = (x-a)q(x) + f(a).
\]
Theorem (Remainder Theorem) If \(a \in \mathbb{F}\) and \(f(x) \in \mathbb{F}[x]\) then \(f(a)\) is the remainder after division of \(f(x)\) by \((x-a)\). That is,
\[
f(x) = (x-a)q(x) + f(a).
\]
Theorem (Factor Theorem) If \(a \in \mathbb{F}\) is a zero of \(f(x)\); that is, if \(f(a) = 0\), then \((x-a)\) is a factor of \(f(x)\). Thus \[ f(x) = (x-a)q(x) \qquad \Longleftrightarrow \qquad f(a) = 0. \]
9.2 Quotient Rings \(\mathbb{F}[x]/\langle p(x) \rangle\)
Def: An integral domain \(R\) is a principal ideal domain (PID) if every ideal is principal, i.e, \(I = \langle a \rangle\) for \(a \in R\).
The next theorem is a consequence of the division algorithm.
Theorem If \(\mathbb{F}\) is a field then \(\mathbb{F}[x]\) is a principal ideal domain. Moreover, if \(I \subseteq \mathbb{F}[x]\) is a nonzero ideal, then \(I = \langle p(x) \rangle\) where \(p(x) \in I\) is any nonzero polynomial of smallest degree in \(I\).
Theorem (Remainders are Unique Coset Representatives) If \[ p(x) = b_0 + b_1 x + \cdots + b_n x^n \in \mathbb{F}[x] \] then the following set is a set of distinct coset representatives for \(\mathbb{F}[x]/\langle p(x) \rangle\). That is, all of the cosets are represented exactly once in this set \[ \frac{\mathbb{F}[x]}{\langle p(x) \rangle} = \{a_0 + a_1 x + \cdots a_{n-1} x^{n-1} + \langle p(x) \rangle \mid a_i \in \mathbb{F}\} \] Moreover, the following coset identity describes multiplication in this quotient ring, \[ x^{n} + \langle p(x) \rangle = \frac{-1}{b_n}(b_0 + b_1 x + b_2 x^2 + \cdots b_{n-1} x^{n-1}) + \langle p(x) \rangle. \]
Theorem If \(\mathbb{F}\) is a field and \(p(x) \in \mathbb{F}[x]\), then the following are equivalent:"
- \(p(x)\) is irreducible (i.e., it does not factor in \(\mathbb{F}[x]\) into a product of two polynomials each of lower degere).
- \(\langle p(x) \rangle \subseteq \mathbb{F}[x]\) is a maximal ideal.
- \(\displaystyle{\mathbb{F}[x]}{\angle p(x) \rangle}\) is a field.
The following theorem can be used to find inverses in \(\mathbb{F}[x]/\langle p(x) \rangle\) in the case when \(p(x)\) is irreducible.
Theorem (Extended Polynomial Euclidean Algorithm) If \(f(x), p(x) \in \mathbb{F}[x]\)