Section 8 Rings

8.1 Definitions

Def: A ring is a set $R$ with two binary operations $+$ and $\ast$ such that:

$R$ is an abelian group under addition. That is,
1. (Identity) There exists $0 \in R$ such that: if $a \in R$, then $a + 0 = 0 + a = a$.
2. (Inverse) If $a \in R$, then there exists $-a \in R$ so that $a + (-a) = 0$.
3. (Associativity) If $a,b,c \in R$, then $(a+b)+c = a + (b+c)$.
4. (Commutative) If $a,b \in R$, then $a+b = b+a$.
(Associativity of product) If $a,b,c \in R$, then $(ab)c = a (bc)$.
(Distributivity) If $a,b,c \in R$, then $a(b+c) = ab + ac$ and $(b+c)a = ba + ca$.

Further Definitions: Let $R$ be a ring.

$R$ is commutative if $ab = ba$ for all $a,b \in R$
$a$ and $b$ are zero divisors if $ab = 0$ and $a\not=0$ and $b \not=0$.
$R$ has unity if there exists an element $1 \in R$ with $a 1 = 1 a = a$.
$u \in R$ is a unit if there exists $u^{-1}$ such that $u u^{-1} = u^{-1} u = 1$.
A commutative ring with unity and no zero divisors is an integral domain.
A commutative ring with unity such that every nonzero element is a unit is a field.

Here is our ring Venn diagram with many of the examples that we have considered.

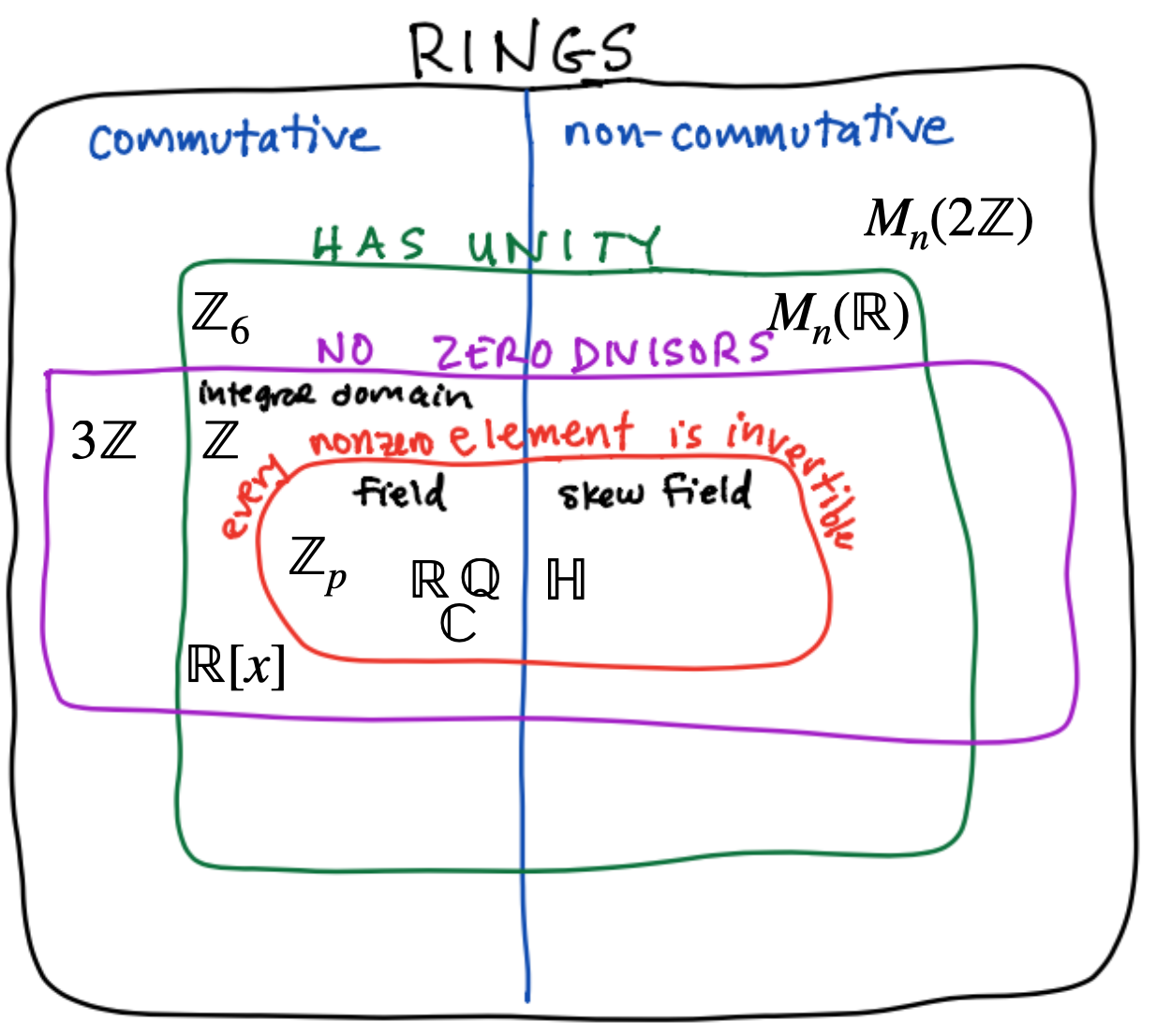
The following basic properties follow by playing the above rules off one another.

Proposition If $R$ is a ring and $a,b,c \in R$, then

$a 0 = 0 a = 0.$
$a (-b) = (-a) b = -ab.$
$(-a)(-b) = ab.$
If $R$ has unity, then $(-1) a = -a$ and $(-1)(-1) =1$.

Proposition: If $R$ is a ring with unity, then the set $U(R)$ set of units in $R$ is a group under multiplication.

Examples:

If $R$ is a commutative ring with unity, then $R$ is a field if and only if $U(R) = R \setminus \{0\}$.
$U(\mathbb{Z}_n) = U(n) = \{ 1 \le k < n \mid \gcd(k,n) = 1 \}$.
$U(\mathbb{Z}) = \{1,-1\}$.
$U(\mathsf{M}_n(RR)) = \mathsf{GL}_n(RR)$.

Proposition: (Cancelation) If $R$ is an integral domain and $a,b,c \in R$ with $a \not=0$, then \[ ab = a c \qquad \Longrightarrow \qquad b = c. \]

Proposition: (Finite Integral Domain) If $R$ is a finite integral domain, then $R$ is a field.

8.2 Subrings, Ideals, and Quotient Rings

Def: If $R$ is a ring, then a subset $S\subseteq R$ is a subring if it is also a ring under the same addition and multiplication as $ R$. To prove that something is a subring, it is enough to verify the following closure properties.

If $a,b \in S$ then $a + b \in S$ (closed under addition).
If $a \in S$, then $-a \in S$ (closed under additive inverses).
If $a,b \in S$, then $ab \in S$ (closed under multiplication).

Def: If $R$ is a ring, then a subset $A\subseteq R$ is an ideal if it is a subring that absorbs products, as follos:

If $a,b \in A$ then $a + b \in A$ (closed under addition).
If $a \in A$, then $-a \in A$ (closed under additive inverses).
If $a \in A$ and $r \in R$ then $ar \in A$ and $ra \in A$ (absorbs products).

Ideals are to Rings what normal subgroups are to groups as the following theorem illustrates.

Theorem If $R$ is a ring and $A \subseteq R$ is an ideal, then coset addition and multiplication, defined by \[ (r + A) + (s + A) = (r+s) + A \qquad\hbox{and}\qquad (r + A) (s + A) = (rs) + A, \] are well defined and they make $R/A$ into a quotient ring. The zero in the quotient ring is $A$, and if $R$ is a ring with unity, then $R/A$ is a ring with unity equal to $1 + A$.

Proposition If $R$ is a ring and $A \subsetneq R$ is a proper ideal, then

If $R$ is commutative, then $R/A$ is commutative
If $1 \in R$ is unity, then $1 + A \in R/A$ is unity.
If $u \in R$ is a unit, then $u + A \in R/A$ is a unit.

Def: If $R$ is a commutative ring and $a \in R$, then the principal ideal generated by $a$ is \[ \langle a Rangle = \{ r a \mid r \in R\}. \] The principal ideal $\langle a Rangle$ is the smallest ideal of $R$ that contains $a$.

Theorem A ring $R$ is a field if and only if the only ideals of $R$ are $\{0\}$ and $R$. That is, a field $R$ is simple: it has no nonzero, proper ideals.

8.3 Prime and Maximal Ideals

8.3.1 Prime Ideals

Def An ideal $A$ is an commutative ring with unity is a prime ideal if it has the property: \[ \text{if}\quad r s \in A \quad \text{ then } \quad r \in A \quad \text{or} \quad s \in A. \] The definition of prime ideal is constructed to make the following theorem work:

Theorem If $A$ is an ideal in a commutative ring $R$ with unity, then \[ R/A \quad\text{is an integral domain} \qquad\text{if and only if}\qquad A \quad\text{is a prime ideal}. \]

8.3.2 Maximal Ideals

Def An ideal $A$ in a ring $R$ is a maximal ideal if it has the property that if $B$ is an ideal with \[ A \subsetneq B \subseteq R, \qquad\text{then}\qquad B = R. \] That is, there are no ideals properly contained bew3een $A$ and $R$.

Theorem If $A$ is an ideal in a commutative ring $R$ with unity, then \[ R/A \quad\text{is a field} \qquad\text{if and only if}\qquad A \quad\text{is a maximal ideal}. \]

8.4 Ring Homomorphisms

Def: A function $\phi: R \to \mathsf{S}$ between rings $R$ and $\mathsf{S}$ is a , if for all $a, b, \in R$, \[ \phi(a + b) = \phi(a) + \phi(b) \qquad\hbox{and}\qquad \phi(a b) = \phi(a) \phi(b). \] If $\phi$ is also a bijection, then it is a ring isomorphism.

The following properties have the same proofs as they did for groups:

Theorem: If $\phi: R \to \mathsf{S}$ is a ring homomorphism,

$\phi(0) = 0$.
If $R$ has unity, 1, then $\phi(1)$ is unity in $\mathsf{S}$
$\phi(n r) = n \phi(r)$; in particular $\phi(-a) = - \phi(a)$.
$\phi(r^n) = \phi(r)^n$
$\phi(R)$ is a subring of $\mathsf{S}$.
If $I \subseteq R$ is an ideal then $\phi(I)$ is an ideal of $\phi(R)$.
If $J \subseteq \mathsf{S}$ is an ideal then $\phi^{-1}(J) = \{r \in R \mid \phi(r) \in J \} \subseteq R$ is an ideal.

Def: The kernel of a ring homomorphism is the set of elements of $R$ that map to $0 \in S$. Thus \[ \mathsf{Ker}(\phi) = \{ r \in \ \mid \phi(r) = 0\}. \]

Theorem: If $\phi: R \to S$ is a ring homomorphism, then $\mathsf{Ker}(\phi)$ is an ideal of $R$ and $\mathsf{Im}(\phi)$ is a subring of $S$.

Theorem (First Fundamental Theorem of Ring Homomorphisms). If $\phi: R \to S$ is a ring homomorphism, then \[ \frac{R}{\mathsf{Ker}(\phi)} \cong \mathsf{Im}(\phi). \] are isomorphic as rings.

Example: If $R$ is an integral domain and $a \in R$, then the evaluation homomorphism is the function \[ \begin{array}{rccl} \phi_a : & R[x] & \to & R \\ & p(x) & \mapsto & p(a) \end{array} \] That is $\phi_a(p(x) ) = p(a)$, so the function “evaluates” every polynomial in $R[x]$ at $x = a$.