Section 7 Group Structure

7.1 Cosets

Def: If \(\mathsf{H}\le \mathsf{G}\) and \(g \in \mathsf{G}\), then the left coset of \(\mathsf{H}\) by \(g\) is the set \[ g \mathsf{H}= \left\{ g h \mid h \in H \right\}, \] and the right coset of \(\mathsf{H}\) by \(g\) is the set \[ \mathsf{H}g = \left\{ h g \mid h \in H \right\}. \]

Example: If \(\mathsf{H}= \{1, (123), (132)\} = \langle (123) \rangle \le {\mathsf{A}}_4\). Then the left cosets and right cosets of \(\mathsf{H}\) are: \[ \begin{array}{rlcrl} \mathsf{H}& = \{1, (123), (132)\} &\qquad& \mathsf{H}& = \{1, (123), (132)\}\\ (124) \mathsf{H}& = \{(124), (14)(23), (134)\}&& \mathsf{H}(124) & = \{(124), (13)(24), (243)\} \\ (142)\mathsf{H}& = \{(142), (234), (13)(24)\} && \mathsf{H}(142) & =\{(142), (143), (14)(23)\}\\ (143)\mathsf{H}& = \{(143), (12)(34), (243)\} && \mathsf{H}(143) & = \{(143), (14)(23), (142)\}\\ \end{array} \]

Theorem (Properties of Cosets): If \(\mathsf{H}\le \mathsf{G}\) and \(a,b, \in \mathsf{G}\), then

1. \(a \in a \mathsf{H}\),
2. \(a \mathsf{H}= \mathsf{H}\) if and only if \(a \in \mathsf{H}\),
3. \(a \mathsf{H}= b \mathsf{H}\) if and only if \(a \in b \mathsf{H}\),
4. \(a \mathsf{H}= b \mathsf{H}\) if and only if \(b^{-1} a \in \mathsf{H}\),
5. \(a \mathsf{H}\cap b \mathsf{H}= \emptyset\) or \(a \mathsf{H}= b\mathsf{H}\),
6. \(|a \mathsf{H}| = |b \mathsf{H}|\).

Parts (a) and (e) tell us that cosets partition the group into a set of disjoint subsets whose union is \(\mathsf{G}\). Part (f) tells us that these subsets all have the same size. This can be pictured as:

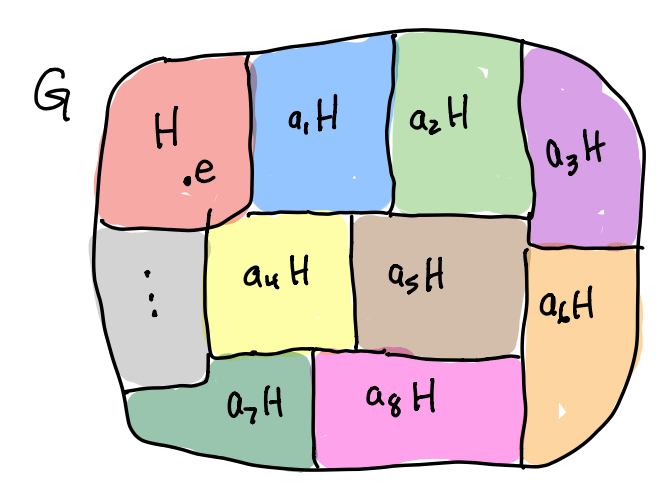
Def: The index of \(\mathsf{H}\) in \(\mathsf{G}\) is \[ [\mathsf{G}:\mathsf{H}] = \#(\text{cosets of } \mathsf{H}\text{ in } \mathsf{G}). \] The following theorem follows immediately from the fact that the cosets partition the group and they are all the same size:

Lagrange’s Theorem: \(|\mathsf{G}| = |\mathsf{H}| [\mathsf{G}:\mathsf{H}]\).

Corollary 1: If \(|\mathsf{G}|\) is finite, then \(|\mathsf{H}|\) divides \(|\mathsf{G}|\) (this is often written as \(|\mathsf{H}|\, \big\vert \,|\mathsf{G}|)\).

Corollary 2: If \(|\mathsf{G}| = p\) (prime), then the only subgroups of \(\mathsf{G}\) are \(\{e\}\) and \(\mathsf{G}\) (i.e, \(\mathsf{G}\) has no nontrivial, proper subgroups).

Corollary 3: If \(g \in \mathsf{G}\), then \(|g| = |\langle g \rangle|\) divides \(|G|\).

Corollary 4: If \(|\mathsf{G}|\) is finite and \(g \in \mathsf{G}\), then \(g^{|\mathsf{G}|} = e\).

Corollary 5: If \(\mathsf{G}\) is finite and \(\mathsf{H}\le \mathsf{K}\le \mathsf{G}\), then \([\mathsf{G}:\mathsf{H}] = [\mathsf{G}:\mathsf{K}] [\mathsf{K}:\mathsf{H}]\).

7.2 Normal Subgroups

Def: A subgroup \(\mathsf{H}\le \mathsf{G}\) is normal if \(g \mathsf{H}= \mathsf{H}g\) for all \(g \in \mathsf{G}\). We write \(\mathsf{H}\trianglelefteq \mathsf{G}\) to indicate that \(\mathsf{H}\) is normal in \(\mathsf{G}\), and we write \(\mathsf{H}\triangleleft \mathsf{G}\) if \(\mathsf{H}\) is a proper normal subgroup of \(\mathsf{G}\) (i.e. \(\mathsf{G}\not= \mathsf{H}\)).

Examples:

1. \(\{e \}\trianglelefteq \mathsf{G}\).
2. \(\mathsf{G}\trianglelefteq \mathsf{G}\).
3. If \(\mathsf{G}\) is abelian, then every subgroup of \(\mathsf{G}\) is normal.
4. The center \(Z(\mathsf{G})\) is a normal subgroup of \(\mathsf{G}\).

Proposition (Normal Subgroup Test): If \(\mathsf{H}\le \mathsf{G}\) then \[ \mathsf{H}\trianglelefteq \mathsf{G}\qquad \text {if and only if } \qquad \text{$g h g^{-1} \in \mathsf{H}$ for all $g \in \mathsf{G}$ and all $h \in \mathsf{H}$}. \]

7.3 Quotient Groups

Def: \(\mathsf{G}/\mathsf{H}= \{ g \mathsf{H}\mid g \in \mathsf{G}\}\) is the set of left cosets of \(\mathsf{H}\) in \(\mathsf{G}\). Note that \[ \left| \frac{\mathsf{G}}{\mathsf{H}} \right| = [\mathsf{G}: \mathsf{H}] = \frac{|\mathsf{G}|}{|\mathsf{H}|}, \] where the second equality only makes sense if \(\mathsf{G}\) is finite.

Def (Coset Multiplication): If \(a \mathsf{H}, b \mathsf{H}\in \mathsf{G}/\mathsf{H}\), then we define \((a \mathsf{H}) (b \mathsf{H}) = ab \mathsf{H}\).

Theorem: If \(\mathsf{H}\trianglelefteq \mathsf{G}\), then coset multiplication is well-defined. That is, if \(a' \in a \mathsf{H}\) and \(b' \in b \mathsf{H}\), then \(a' b' \mathsf{H}= ab \mathsf{H}\). This makes coset multiplication a binary operation on \(\mathsf{G}/\mathsf{H}\).

Therefore, if \(\mathsf{H}\trianglelefteq \mathsf{G}\), then the set of cosets \(\mathsf{G}/\mathsf{H}\) forms a group under coset multiplication. Such that

1. The identity is \(e \mathsf{H}= \mathsf{H}\) since \((e \mathsf{H}) (g \mathsf{H}) = e g \mathsf{H}= g \mathsf{H}\).
2. The inverse of \(g \mathsf{H}\) is \(g^{-1} \mathsf{H}\) since \((g \mathsf{H}) (g^{-1} \mathsf{H}) = g g^{-1} \mathsf{H}= \mathsf{H}\).

7.4 Homomorphisms

Def: If \(\mathsf{G}\) and \(\mathsf{H}\) are groups, then a homomorphism from \(\mathsf{G}\) to \(\mathsf{H}\) is a function \(\phi: \mathsf{G}\to \mathsf{H}\) such that, if \(a,b \in \mathsf{G}\), then \[ \phi( a b) = \phi(a) \phi(b). \] Theorem (Properties of Homomorphisms): if \(\phi: \mathsf{G}\to \mathsf{H}\) is a homomorphism, and \(g \in \mathsf{G},\) then

1. \(\phi(e_\mathsf{G}) = e_\mathsf{H}\).
2. \(\phi(g^{-1}) = \phi(g)^{-1}\)
3. \(\phi(g^k) = \phi(g)^k\) for all \(k \in \mathbb{Z}\)
4. \(|\phi(g)|\, \Big\vert\, |g|\)
5. If \(K \le \mathsf{G}\) then \(\phi(\mathsf{K}) \le H\) where \(\phi(\mathsf{K}) = \{ \phi(k) \mid k \in \mathsf{K}\}\).

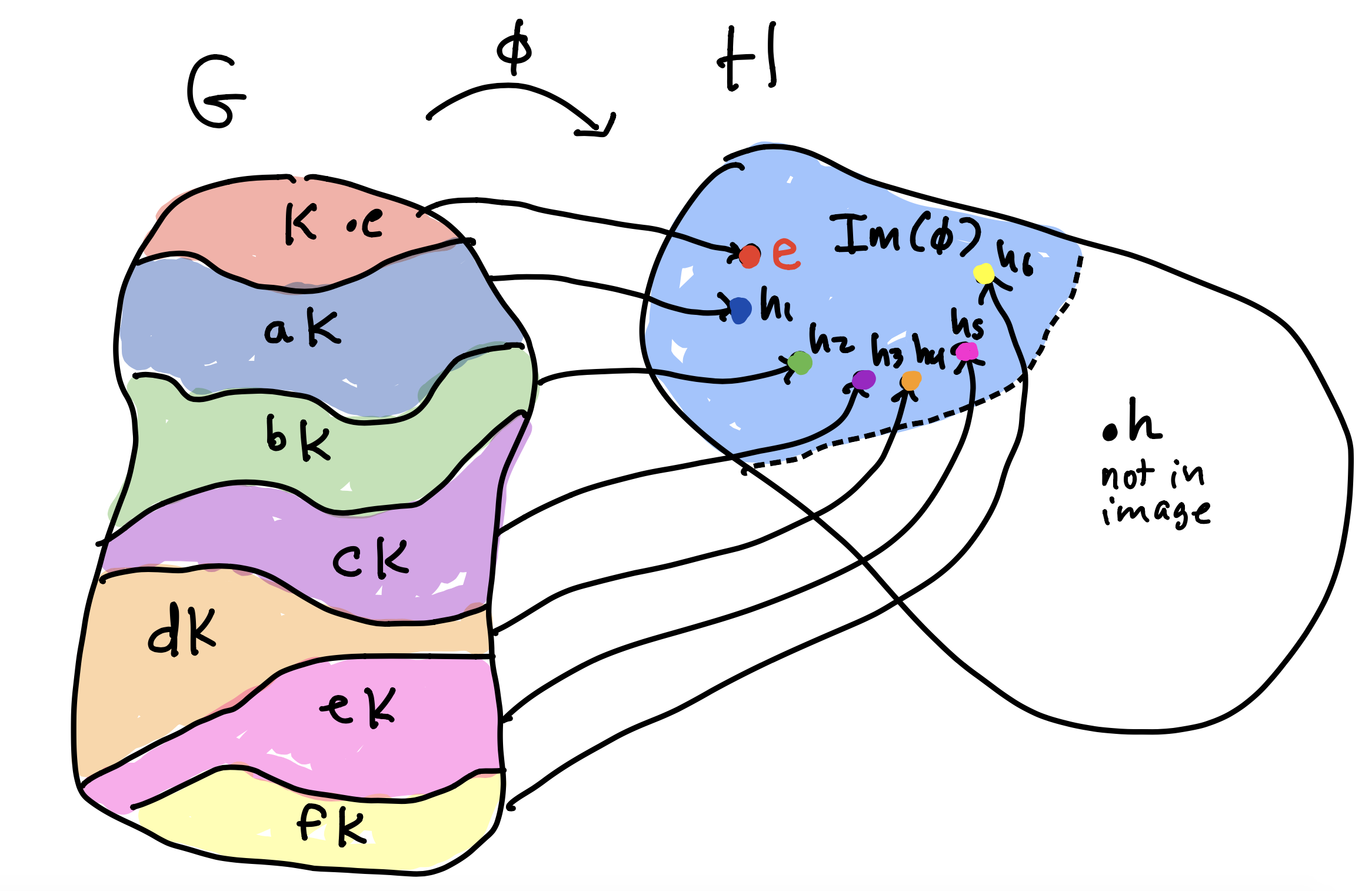
Def: if \(\phi: \mathsf{G}\to \mathsf{H}\) is an homomorphism, then the kernel and image of \(\phi\) are the following subsets of \(\mathsf{G}\) and \(\mathsf{H}\), respectively, \[\begin{align*} \mathsf{Ker}(\phi) &= \{ g \in \mathsf{G}\mid \phi(g) = e_H\} \\ \mathsf{Im}(\phi) &= \{ h \in \mathsf{H}\mid \text{there is at least one } g \in \mathsf{G}\text{ such that } \phi(g) = h \} \\ &= \{ \phi(g) \mid g \in \mathsf{G}\} \end{align*}\]

Theorem. If \(\phi: \mathsf{G}\to \mathsf{H}\) is a group homomorphism, then

1. \(\mathsf{Ker}(\phi) \trianglelefteq \mathsf{G}\),
2. \(\mathsf{Im}(\phi) \leq \mathsf{H}\).

Proposition. (Kernel Cosets): If \(\phi: \mathsf{G}\to \mathsf{H}\) is a group homomorphism, \(\mathsf{K}= \mathsf{Ker}(\phi)\), and \(a,b\in\mathsf{G}\), then \[ a \mathsf{K}= b \mathsf{K}\quad \Leftrightarrow \quad \phi(a) = \phi(b). \] Def: If \(\phi: \mathsf{G}\to \mathsf{H}\) is a group homomorphism and \(h \in \mathsf{H}\), then the fiber of \(h\) is the following subset of \(\mathsf{G}\): \[ \phi^{-1}(h) = \{g \in \mathsf{G}\mid \phi(g) = h\}. \] That is, these are the elements of \(\mathsf{G}\) that map to \(h\).

The previous proposition tells us:

Corollary: If \(\phi: \mathsf{G}\to \mathsf{H}\) is a homomorphism with kernel \(\mathsf{K}\), then

1. If \(\phi(g) = h\), then \(\phi^{-1}(h) = g \mathsf{K},\)
2. \(\phi\) is \(|\mathsf{K}|\)-to-one,
3. \(\phi\) is one-to-one if and only if \(\mathsf{K}= \{e\}\).

Example. The function \(\phi: \mathsf{D}_{6} \to \mathbb{Z}_2 \times \mathbb{Z}_2\) given by \(r \mapsto (1,0)\) and \(f \mapsto (0,1)\) is a homomorphism. The fibers, and thus \(\mathsf{Ker}(\phi)\)-cosets, of this function are as follows: \[ \begin{array}{ccc} \phi^{-1}(h) & & h \\ \hline \mathsf{K}= \{ 1, r^2, r^4 \} & \mapsto & (0,0) \\ r \mathsf{K}= \{ r, r^3, r^5 \} & \mapsto & (1,0) \\ f \mathsf{K}= \{ f, r^2 f, r^4f \} & \mapsto & (0,1) \\ rf \mathsf{K}= \{ rf, r^3 f, r^5 f \} & \mapsto & (1,1) \\ \end{array} \] We see that \(\mathsf{D}_6/\mathsf{K}\cong \mathbb{Z}_2 \times \mathbb{Z}_2\) as the next Theorem says in general.

Theorem. (First Isomorphism Theorem): If \(\phi: \mathsf{G}\to \mathsf{H}\) is a group homomomorphism, then the following map is an isomorphism, \[ \displaystyle{\frac{\mathsf{G}}{\mathsf{Ker}(\phi)}} \cong \mathsf{Im}(\phi), \] and the isomorphism is given by sending the coset \(a \mathsf{Ker}(\phi)\) to \(\phi(a)\).

7.5 Group Actions

Def: If \(\mathsf{G}\) is a group and \(X\) is a set, then there is an action of \(\mathsf{G}\) on \(X\) if for every \(g \in \mathsf{G}\) and \(x \in X\) we can define \(g \cdot x \in X\) so that

1. If \(x \in X\), then \(e \cdot x = x\).
2. If \(x \in X\) and \(g, h \in \mathsf{G}\), then \((g h) \cdot x = g \cdot ( h \cdot x)\).

Examples. We’ve seen many of these:

1. The symmetric group \(\mathsf{S}_n\) acts on the set \(X = \{1,2,3, \ldots n\}\) by permuting the elements of the set.

2. The general linear group \(GL_n(\mathbb{R})\) acts on the set ov vectors \(X = \mathbb{R}^n\) by the matrix vector product \(A v.\)

3. The dihedral group \(\mathsf{D}_n\) of symmetries of an \(n\)-gon acts on the sets of vertices \(V\) and on the set of edges \(E\) of the \(n\)-gon.

4. Any group \(\mathsf{G}\) acts on itself \(X = \mathsf{G}\) by left (or right) multiplication: \(g \cdot x = gx\).

5. Any group \(\mathsf{G}\) acts on itself \(X = \mathsf{G}\) by conjugation: \(g \cdot x = gxg^{-1}\).

6. Any subgroup \(\mathsf{H}\le \mathsf{G}\) acts on \(X=\mathsf{G}\) by left (or right) multiplication: \(h \cdot g = h g\).

7. A group \(\mathsf{G}\) acts on its subgroups \(\{ \mathsf{H}\mid \mathsf{H}\le \mathsf{G}\}\) by conjugation: \(g \cdot \mathsf{H}= g \mathsf{H}g^{-1}\) (see Conjugate Subgroups).

Def: The stabilizer and orbit of a group action are the sets \[ \mathsf{Stab}_\mathsf{G}(x) = \{ g \in G \mid g \cdot x = x \} \le \mathsf{G}\hskip.3in \mathsf{G}x = \{ g \cdot x \mid g \in \mathsf{G}\} \subseteq X. \]

Theorem: The stabilizer is a subgroup of \(\mathsf{G}\).

Theorem (Orbit-Stabilizer): If \(\mathsf{G}\) acts on \(X\) and \(x \in X\), and \(S = \mathsf{Stab}_\mathsf{G}(x)\), then

1. \(|\mathsf{G}| = |S| | \mathsf{G}x|\). In particular \([\mathsf{G}:S] = |\mathsf{G}x|\).

2. If \(g \cdot x = y\), then $ g S = { h h x = y }$.