Section 23 Complex Eigenvalues

Now we will explore what happens if the matrix has complex eigenvalues.

23.1 Rotation-Dilation

First we explore a special case of 2x2 matrices with complex eigenvalues of the following form: \[ R=\begin{bmatrix} a & -b \\ b & a \\ \end{bmatrix} \] As we see in the image below, this matrix rotates by angle of \(\theta\) and expands (dilates) or contracts by a factor of \(r\) where \[ \begin{align} \theta &= \arctan(b/a) \\ r &= \sqrt{a^2 + b^2} \end{align} \]

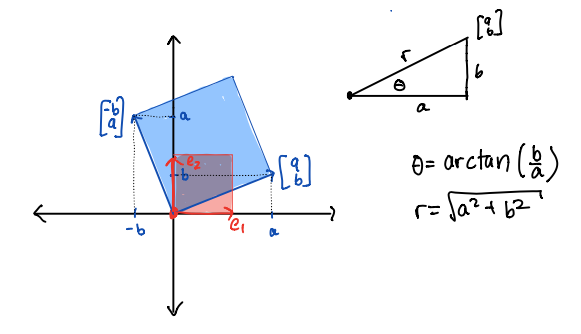
Furthermore the eigenvalues of this matrix are the complex values \[ \lambda_1 = a + b i \qquad \lambda_2 = a - b i \] where \(i = \sqrt{-1}\). These eigenvalues are conjugate pairs and are often written as \(\lambda = a \pm b i\). They come from applying the quadratic formula to the characteristic polynomial and getting a negative discriminant under the square root. It is important to note that both the angle of rotation \(\theta\) and the dilation factor \(r\) are contained in the eigenvalues. The fact that these are the eigenvalues is derived in the video. We will illustrate it here in three examples.

23.1.1 Example 1

Our first example has \(a = .9\) and \(b = .2\).

##      [,1] [,2]
## [1,]  0.9 -0.2
## [2,]  0.2  0.9

We look at its eigenvectors and eigenvalues and see that \(\lambda = .9 \pm .2 i\):

eigen(A)

## eigen() decomposition
## $values
## [1] 0.9+0.2i 0.9-0.2i
## 
## $vectors
##                      [,1]                 [,2]
## [1,] 0.7071068+0.0000000i 0.7071068+0.0000000i
## [2,] 0.0000000-0.7071068i 0.0000000+0.7071068i

Notics that the eigenvectors also come in conjugate pairs, with a real and a complex part. This always happens. \[ \vec{\mathsf{v}} = \begin{bmatrix}0.707 \\ 0.000 \end{bmatrix} \pm \begin{bmatrix} 0.000 \\ .707 \end{bmatrix} i \] Now, let’s find the angle of rotation. We will use the Arg command which finds the angle (in radians) of a complex number. We also convert it to degrees here.

vals = eigen(A)$values
v1 = vals[1]
Arg(v1)  # gives the argument, or angle, of a complex number (in radians)

## [1] 0.2186689

Arg(v1) / (2*pi) * 360 # convert to degrees

## [1] 12.52881

For good measure, we can compare with using the arctan function.

atan(.2/.9)

## [1] 0.2186689

Next we find the dilation/contraction factor. We can do so using the Mod command, which finds the “modulus” or absolute value or length of a complex number.

Mod(v1) # gives the length of a complex number

## [1] 0.9219544

And, again for good measure, we compare with using the Pythagorean theorem:

sqrt(.9^2 + .2^2)

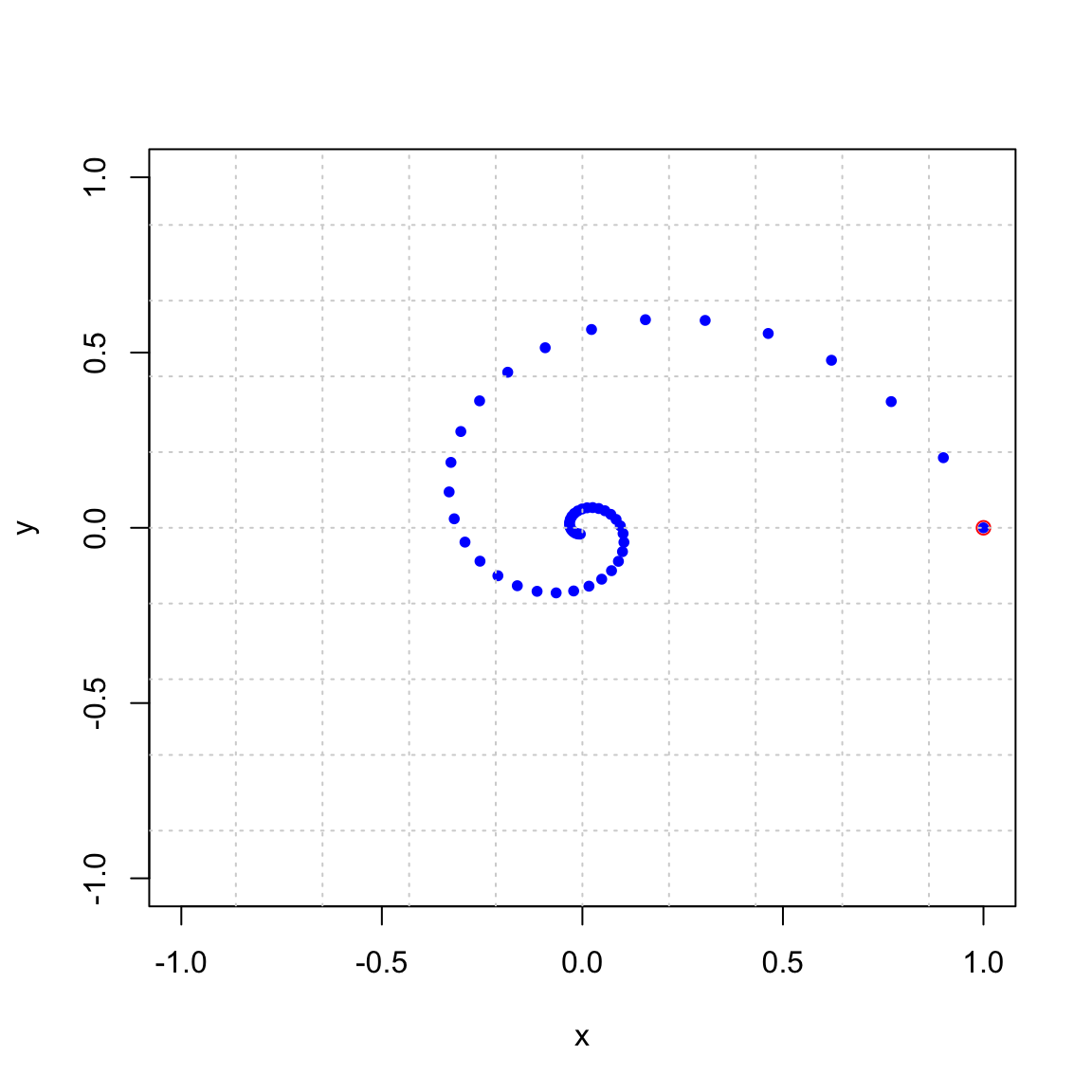
## [1] 0.9219544

Now, we observe the trajectory of a single point \((0,1)^T\) under this matrix. In this picture you can see that it is contracting and rotating by 12.5 degrees. Note that 360/12.5 is about 29, and it takes 29 applications to go once around the circle. You can count them in the plot below. Furthermore, \((0.9219544)^29 =0.095\) and after 29 applications the vector is about 1/10 of its original length.

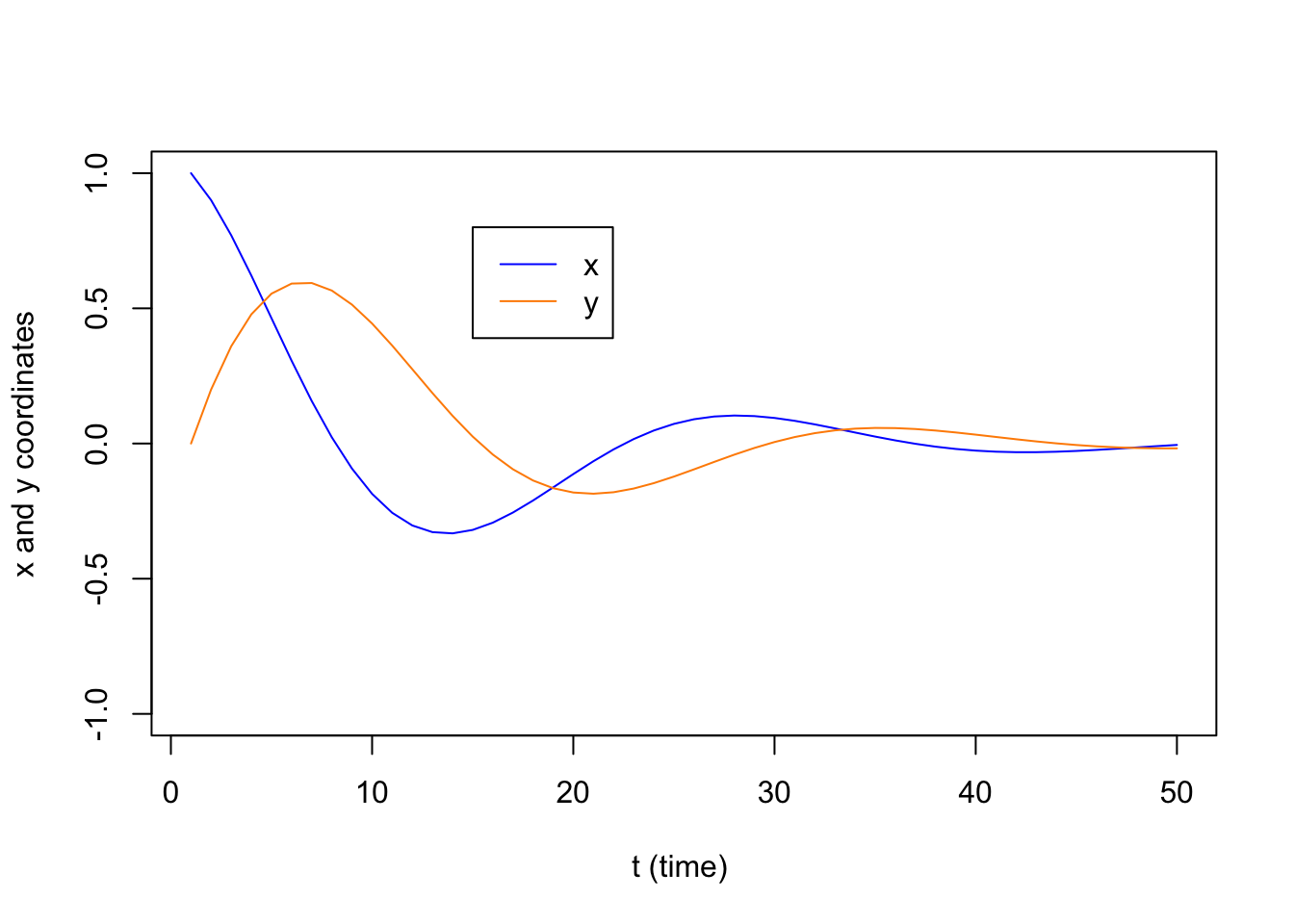
We can also view this by looking at a plot of the x and y coordinates over time as the point (x,y) circles around in the xy-plane. Key point: complex eigenvalues lead to oscillating values of the individual coordinates

We can also use trajectory_plot from Dynamical Systems in 2D to watch what happens to a whole grid of points under this transformation. It is beautiful!

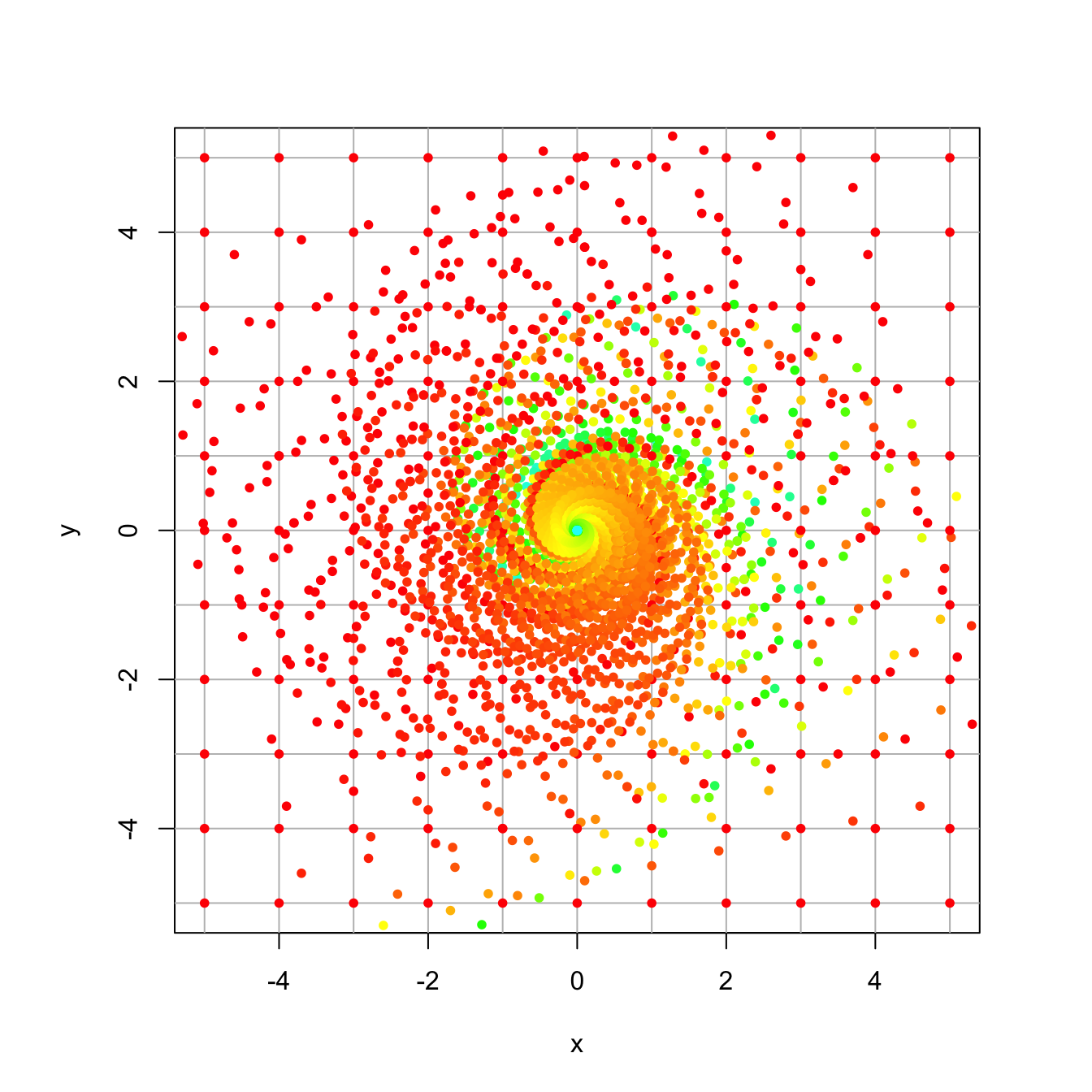
trajectory_plot(A, t=30, datamax=5, plotmax=5, numpoints=10)

23.1.2 Example 2

Here is a second example of a rotation-dilation matrix, this time with \(a = .96\) and \(b = .28\).

(A = cbind(c(.96,.28),c(-.28,.96)))

##      [,1]  [,2]
## [1,] 0.96 -0.28
## [2,] 0.28  0.96

eigen(A)

## eigen() decomposition
## $values
## [1] 0.96+0.28i 0.96-0.28i
## 
## $vectors
##                      [,1]                 [,2]
## [1,] 0.7071068+0.0000000i 0.7071068+0.0000000i
## [2,] 0.0000000-0.7071068i 0.0000000+0.7071068i

We check the angle of rotation and the dilation factor

vals = eigen(A)$values
v1 = vals[1]
Arg(v1)  # gives the argument, or angle, of a complex number (in radians)

## [1] 0.2837941

Arg(v1) / (2*pi) * 360 # convert to degrees

## [1] 16.2602

Mod(v1)  # gives the length of a complex number

## [1] 1

Notice that the dilation factor is 1, which is seen in the following plots. Here are 21 iterations:

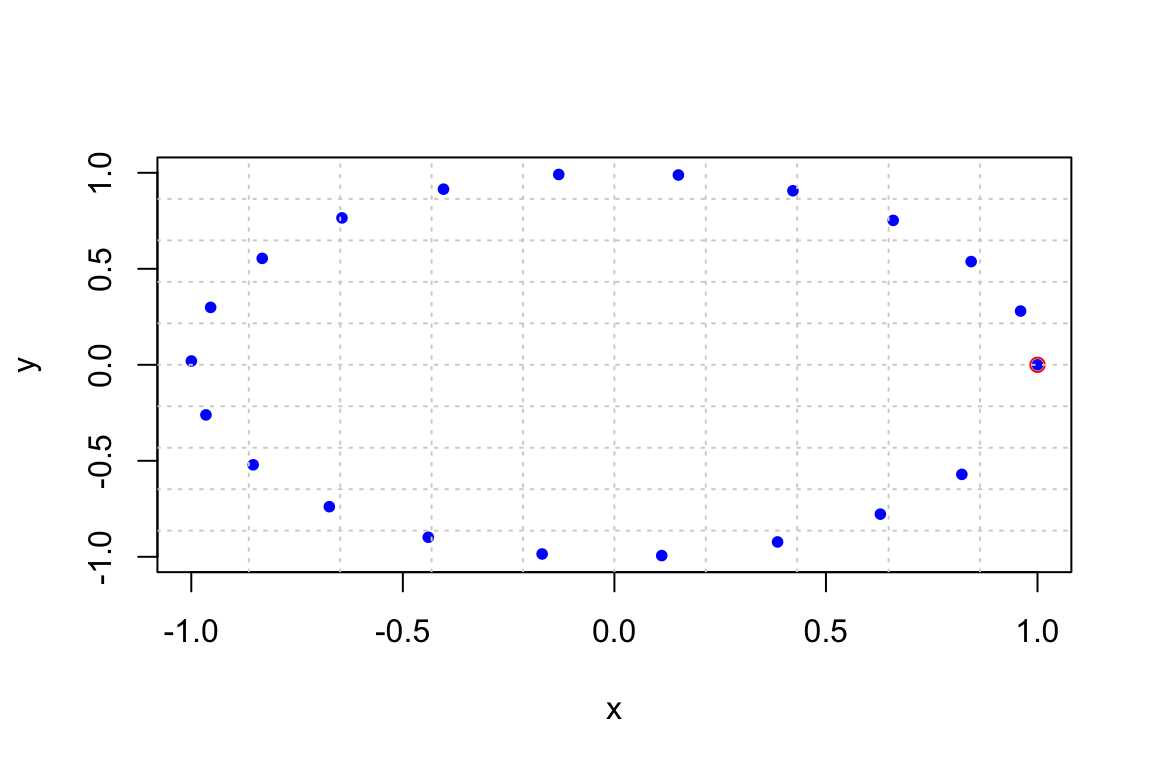
And here are 200 iterations

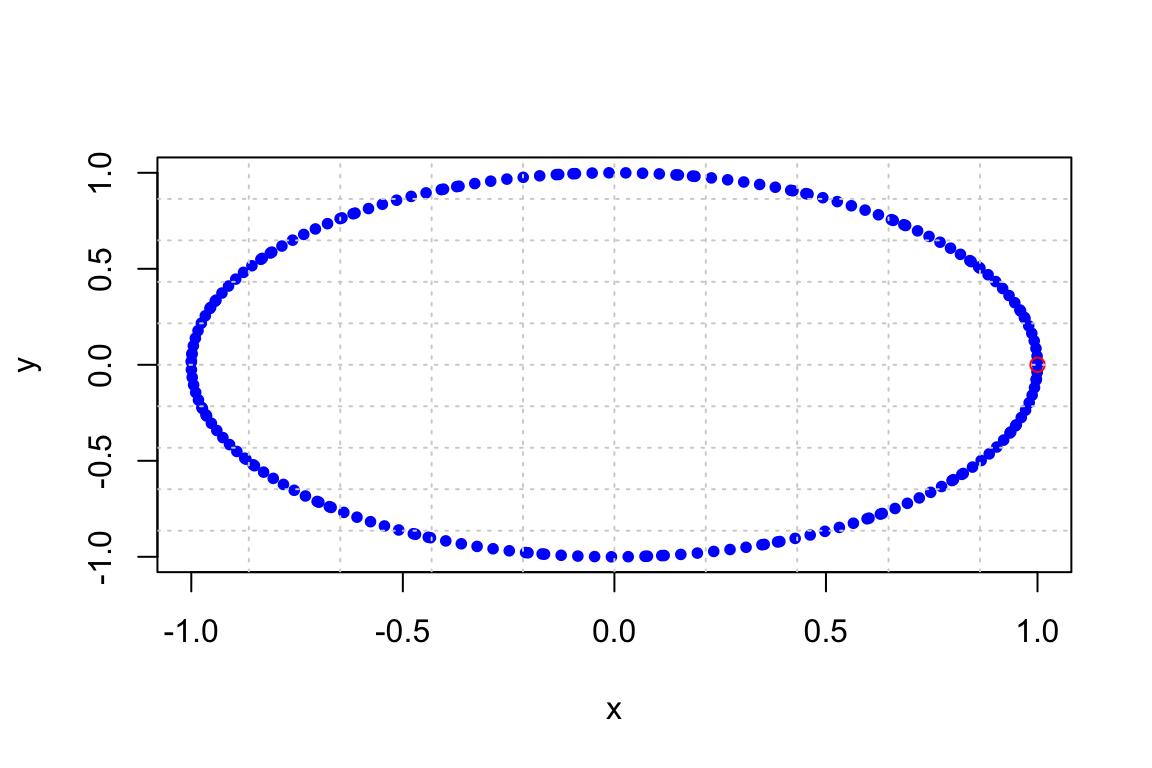
And a trajectory plot:

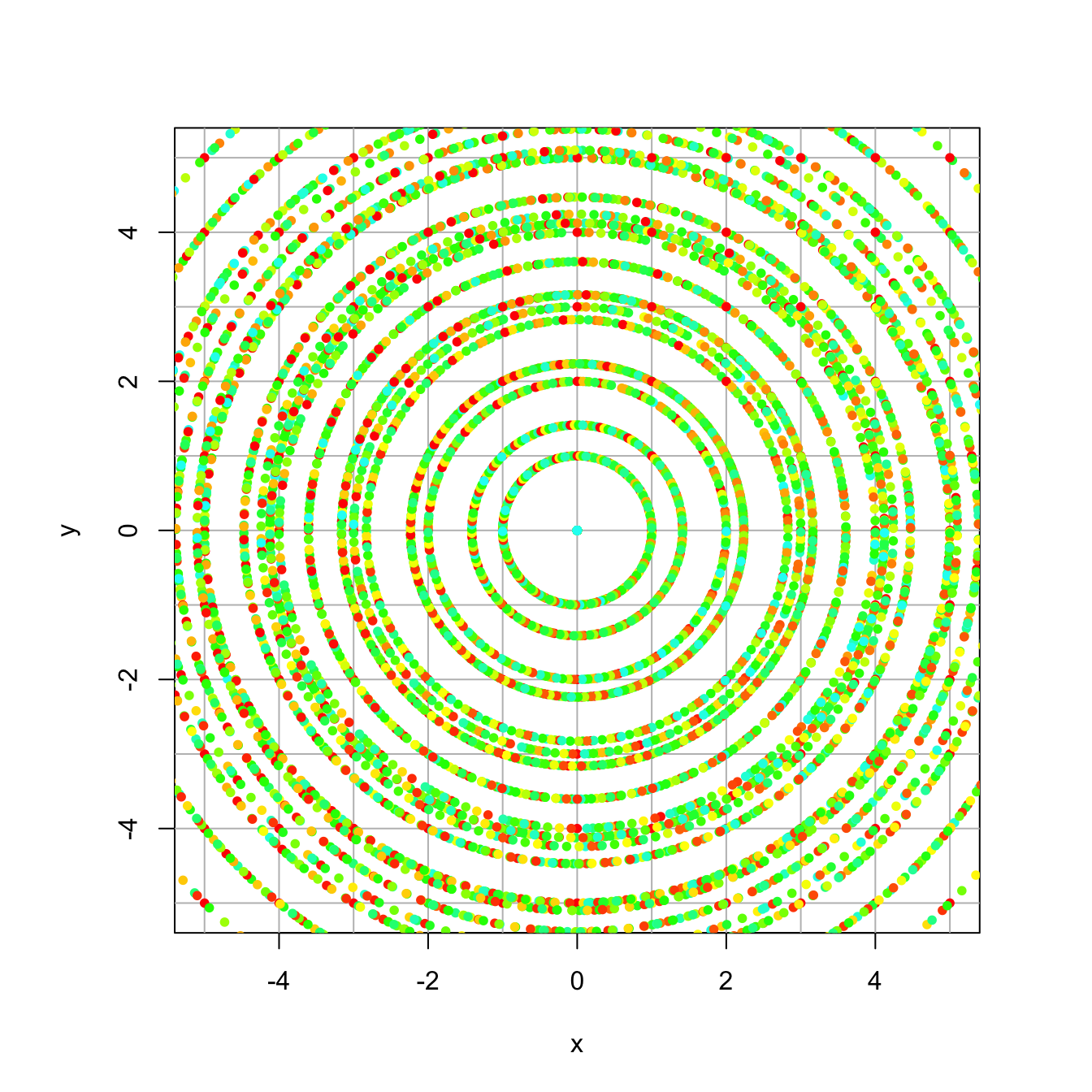
23.1.3 Example 3

A third and final example.

(A = cbind(c(.99,.16),c(-.16,.99)))

##      [,1]  [,2]
## [1,] 0.99 -0.16
## [2,] 0.16  0.99

eigen(A)

## eigen() decomposition
## $values
## [1] 0.99+0.16i 0.99-0.16i
## 
## $vectors
##                       [,1]                  [,2]
## [1,]  0.0000000-0.7071068i  0.0000000+0.7071068i
## [2,] -0.7071068+0.0000000i -0.7071068+0.0000000i

vals = eigen(A)$values
v1 = vals[1]
Arg(v1) / (2*pi) * 360 # convert to degrees

## [1] 9.180542

Mod(v1)  # gives the length of a complex number

## [1] 1.002846

We see that the dilation factor is \(r = 1.0028\) and the angle of rotation is \(9.18\) degrees. Here are 100 iterations.

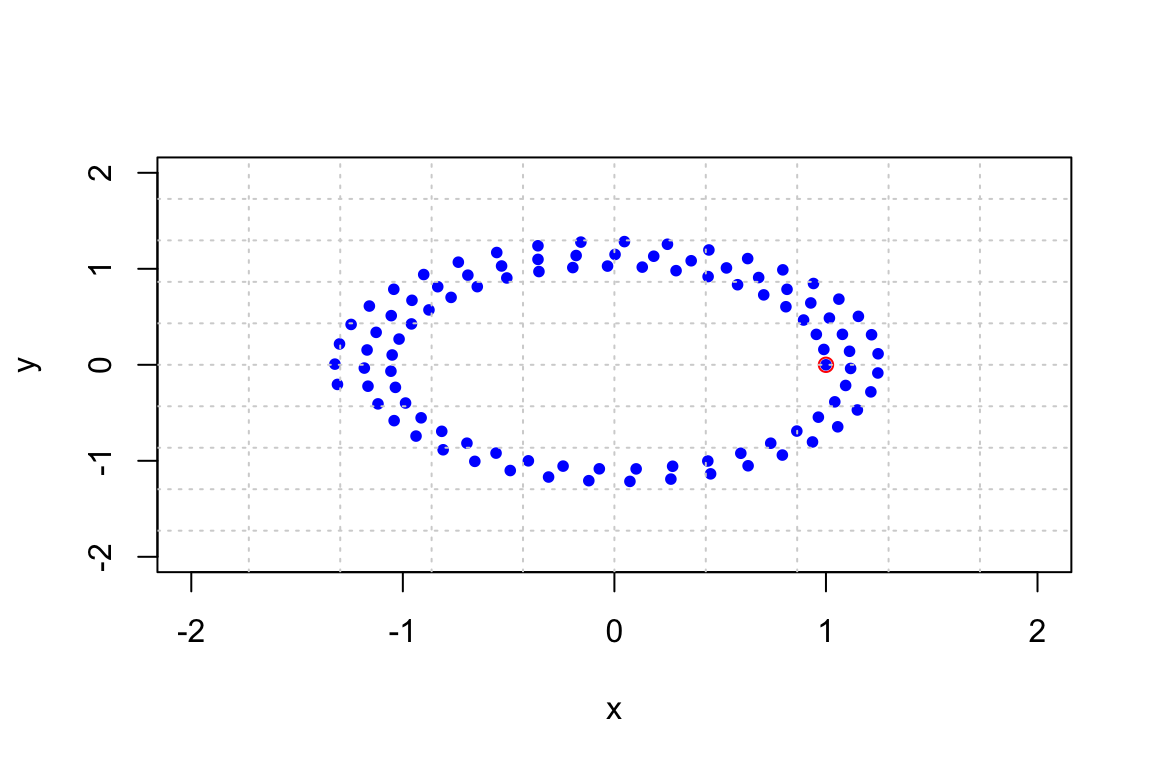
And a trajectory plot:

23.2 General 2x2 Matrices with Complex Eigenvalues

Now suppose we have a 2x2 matrix with complex eigenvalues \(\lambda = a \pm b i\) and complex eigenvectors \(\mathsf{v} = \mathsf{u } \pm \mathsf{w} i\) that is not in rotation-dilation form. Here is an example: \[ A = \begin{bmatrix} 1.19 & -0.38 \\ 0.29 & 0.78 \end{bmatrix} \] It has eigenvalues and eigenvectors \[ \lambda = 0.985 \pm 0.261 i \qquad \mathsf{v} = \begin{bmatrix} 0.753 \\ 0.406 \end{bmatrix} \pm \begin{bmatrix} 0.000 \\ -0.517 \end{bmatrix} i \] as seen here:

##      [,1]  [,2]
## [1,] 1.19 -0.38
## [2,] 0.29  0.78

## eigen() decomposition
## $values
## [1] 0.985+0.2611034i 0.985-0.2611034i
## 
## $vectors
##                      [,1]                 [,2]
## [1,] 0.7531030+0.0000000i 0.7531030+0.0000000i
## [2,] 0.4062793-0.5174679i 0.4062793+0.5174679i

The angle of rotation and factor of dilation are \(\theta = 14.8\) degrees and \(r = 1.019\) as we see from these computations:

## [1] 14.84649

## [1] 1.019019

A trajectory plot shows us that it is still rotating by 14.8 degrees and dilating by 1.019, but it is taking more of an elliptical pattern.

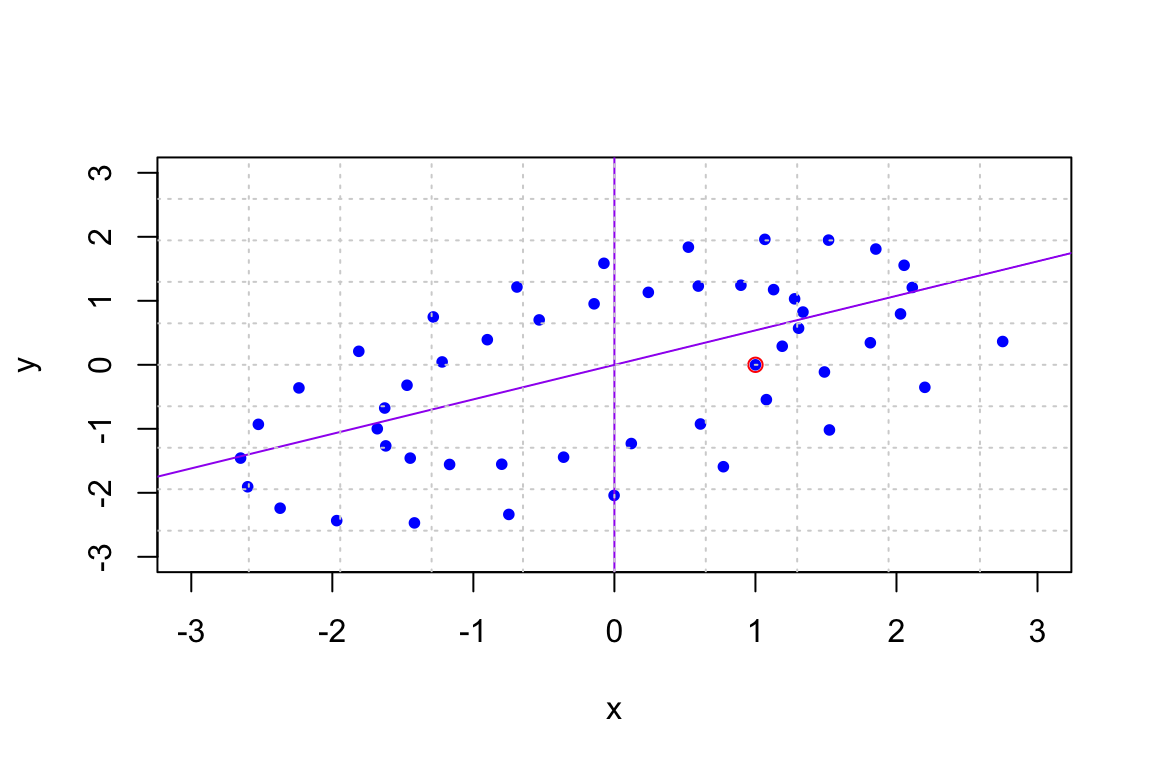
To see precisely what happens, we change to basis \(\{\mathsf{w}, \mathsf{u}\}\) where \(\mathsf{w}\) and \(\mathsf{u}\) are the imaginary and real parts of the eigenvector \(\mathsf{v} =\mathsf{u} + \mathsf{w} i\). In this case the eigenvalues and eigenvectors are \[ \lambda = 0.985 \pm 0.261 i \qquad \mathsf{v} = \begin{bmatrix} 0.753 \\ 0.406 \end{bmatrix} \pm \begin{bmatrix} 0.000 \\ -0.517 \end{bmatrix} i \] So if we make the change of basis matrix \(P = [\mathsf{u},\mathsf{w}]\) \[ P = \begin{bmatrix} 0.000 & 0.753 \\ -0.517 & 0.406 \end{bmatrix} \] then we can factor \(A\) as \[ A = \begin{bmatrix} 1.19 & -0.38 \\ 0.29 & 0.78 \end{bmatrix} = \underbrace{\begin{bmatrix}0.000 & 0.753 \\-0.517 & 0.406 \end{bmatrix}}_P \underbrace{\begin{bmatrix} 0.985 & - 0.261 \\ 0.261 & 0.985 \end{bmatrix}}_R \underbrace{\begin{bmatrix}0.000 & 0.753 \\-0.517 & 0.406 \end{bmatrix}^{-1}}_{P^{-1}} \] We have not diagonalized \(A\). Rather we have rotation-dilationalized (made up term) the matrix \(A\). At is core \(A\) is a rotation-dilation matrix whose angle and dilation factor come from the eigenvalue. The matrix \(P\) is a change of basis matrix. It is rotating and dilating in this new coordinate system, which are the vectors in the plot above.

If we multiply the other way, we get \[ P^{-1} A P = \begin{bmatrix} 0.985 & - 0.261 \\ 0.261 & 0.985 \end{bmatrix} = R \] Which we can see using R

##            [,1]      [,2]
## [1,]  0.0000000 0.7531030
## [2,] -0.5174679 0.4062793

##           [,1]       [,2]
## [1,] 0.9850000 -0.2611034
## [2,] 0.2611034  0.9850000

23.3 A 3D example

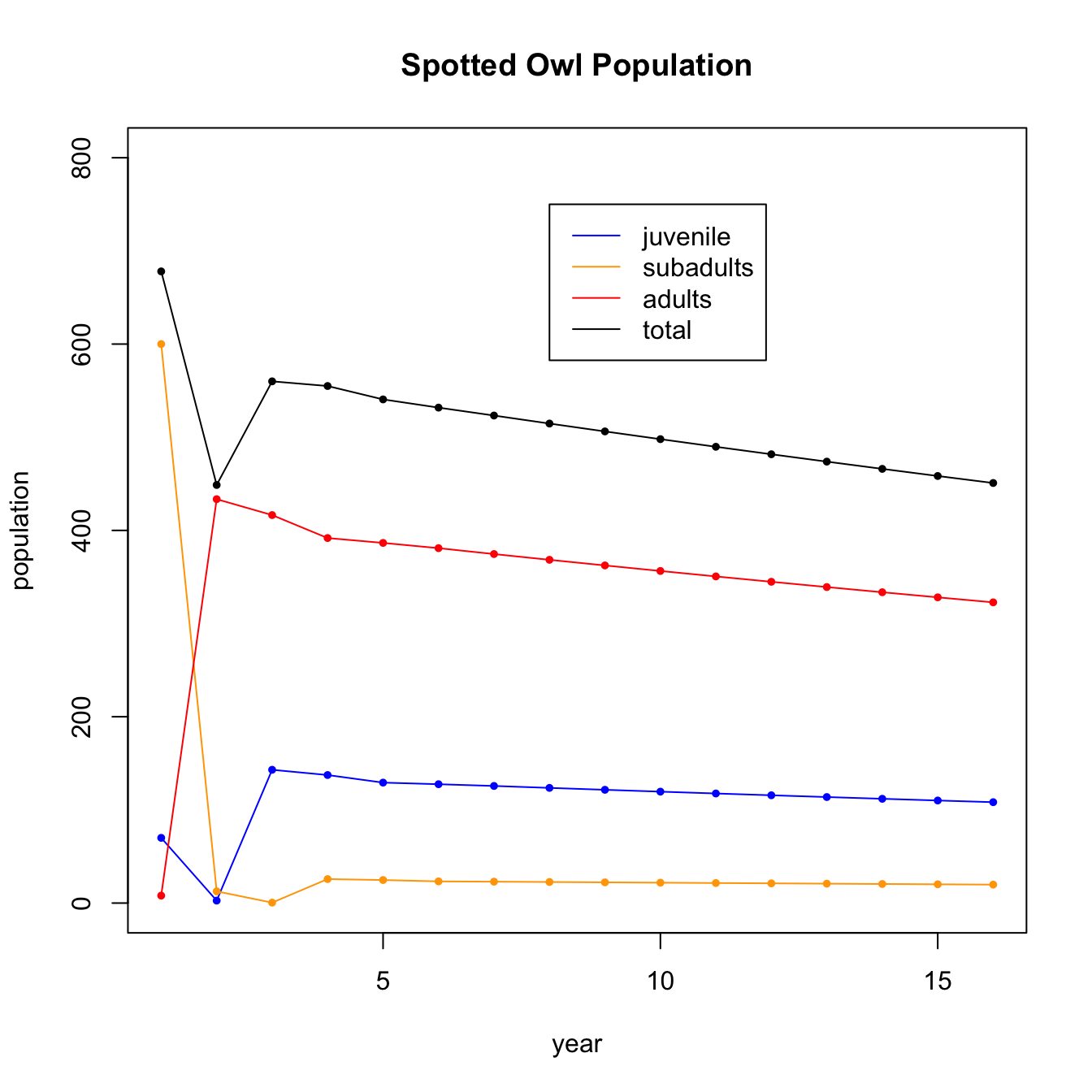
Here is the Northern Spotted Owl matrices from the [Eigenvalues] examples. We saw that it has one real and two complex eigenvalues:

## eigen() decomposition
## $values
## [1]  0.9835927+0.0000000i -0.0217964+0.2059185i -0.0217964-0.2059185i
## 
## $vectors
##               [,1]                  [,2]                  [,3]
## [1,] 0.31754239+0i  0.6820937+0.0000000i  0.6820937+0.0000000i
## [2,] 0.05811107+0i -0.0624124-0.5896338i -0.0624124+0.5896338i
## [3,] 0.94646180+0i -0.0450520+0.4256233i -0.0450520-0.4256233i

The eigenvalues are always listed in descending order by magnitude as we see here when we compute their modulus and arguments

## [1] 0.9835927 0.2070688 0.2070688

## [1]   0.00000  96.04223 -96.04223

We can diagonalize this over the complex numbers.

##              [,1]                  [,2]                  [,3]
## [1,] 0.9835927+0i  0.0000000+0.0000000i  0.0000000+0.0000000i
## [2,] 0.0000000+0i -0.0217964+0.2059185i  0.0000000+0.0000000i
## [3,] 0.0000000+0i  0.0000000+0.0000000i -0.0217964-0.2059185i

It has complex eigenvalues on the diagonal and requires using the complex vectors in our basis. Often, this is not what we want to do if our matrix has real entries and comes from a real-valued problem.

Instead, let’s rotation-dilationalize this matrix. The block diagonalization consists of a 1x1 block of the real eigenvalue and a 2x2 block of the rotation-dilation part of the complex eigenvalues.

##            [,1]       [,2]        [,3]
## [1,] 0.31754239  0.0000000  0.68209367
## [2,] 0.05811107 -0.5896338 -0.06241245
## [3,] 0.94646180  0.4256233 -0.04505202

##           [,1]       [,2]       [,3]
## [1,] 0.9835927  0.0000000  0.0000000
## [2,] 0.0000000 -0.0217964 -0.2059185
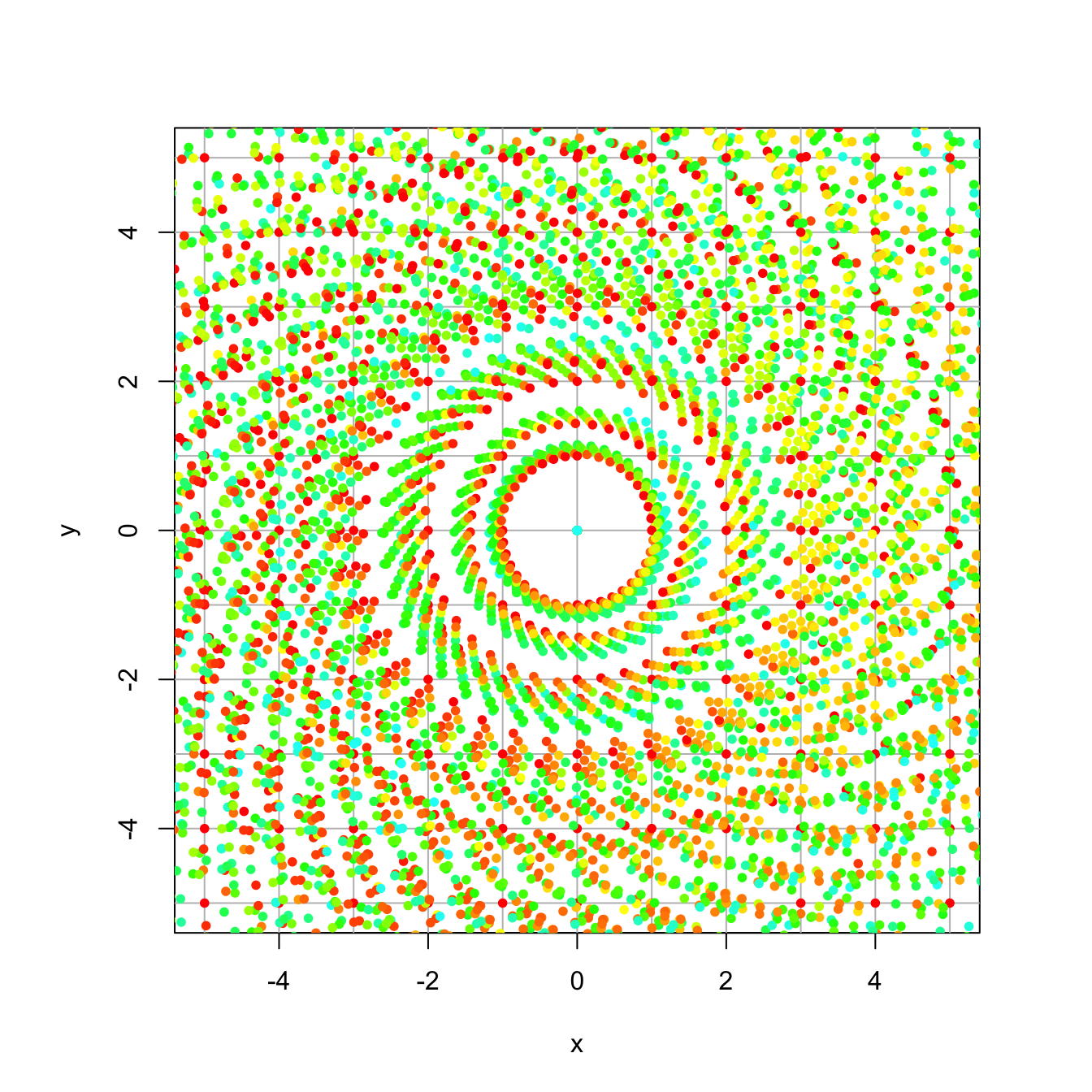
## [3,] 0.0000000  0.2059185 -0.0217964

In 3 dimensions, there the geometry is as follows: * there is one basis vector, corresponding to the real eigenvalue \(\lambda = 0.985\) * there is a plane in which the system rotates by \(\theta = 96\) degrees and contracts by \(r = 0.207\). * thus, the complex part dies off pretty quickly (\(r = 0.207\)), and it converges to the dominant real eigenvector, which is also dying off but more slowly (\(r = 0.983\))

We can see this in the traectory plot below. The oscillating part at the beginning comes from the complex eigenvalues as they quickly die off and the system converges to the dominant real eigenvector.