Section 2 Problem Set 2
- Due: Tuesday February 2 by 10:00am CST.
- Upload your solutions to Moodle in a PDF.
- Please feel free to use RStudio for all row reductions.
- In problems where you use RStudio for row reduction and are not asked to turn in an R markdown file, you can write something like this:
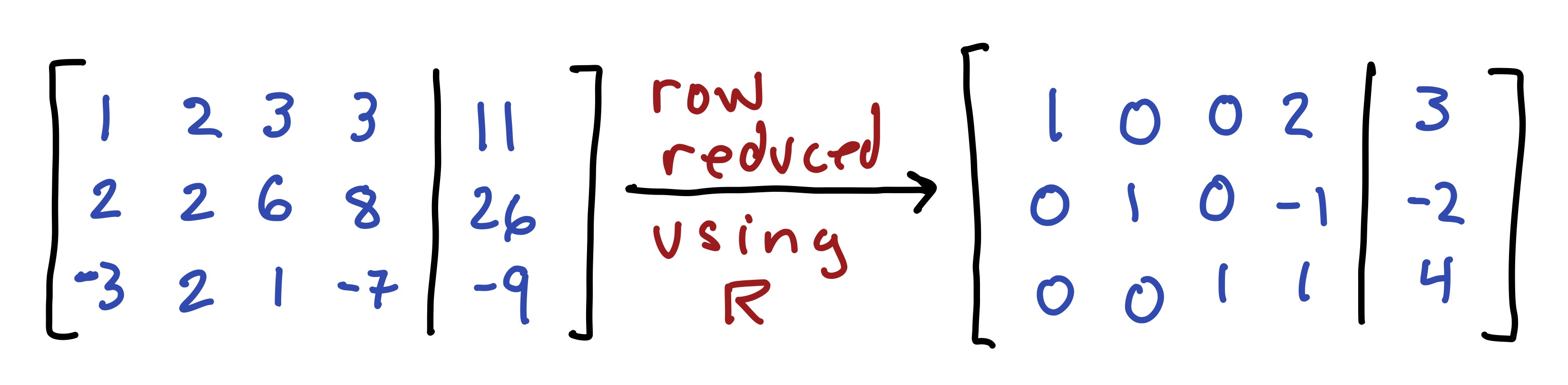
- You can download the Rmd source file for this problem set.
The Problem Set covers sections 1.3, 1.4, 1.5, and 1.7.
2.1 Parametric Vector Form
Here is the augmented matrix for a system of linear equations \(\mathsf{A} \mathsf{x} = \mathsf{b}\), and its RREF. Give the general solution to this system in parametric vector form.
\[ \left[ \begin{array}{ccccc|c} 1 & 1 & -1 & -1 & 2 & 1 \\ 1 & 0 & -2 & 1 & 1 & 3 \\ -2 & 1 & 5 & 1 & -6 & 2 \\ -3 & 0 & 6 & 2 & -8 & 1 \\ 0 & 1 & 1 & 2 & -3 & 6 \\ 1 & 0 & -2 & -1 & 3 & -1 \\ \end{array} \right] \longrightarrow \left[ \begin{array}{ccccc|c} 1 & 0 & -2 & 0 & 2 & 1 \\ 0 & 1 & 1 & 0 & -1 & 2 \\ 0 & 0 & 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \]
2.2 RREF for a linear system
Here is the reduced row echelon form of a matrix \(\mathsf{A}\) (you are not given the matrix \(\mathsf{A}\)). \[ \mathsf{A} \longrightarrow \left[ \begin{array}{cccc} 1 & -2 & 0 & 4 \\ 0 & 0 & 1 & -5 \\ 0 & 0 & 0 & 0 \\ \end{array} \right] \]
Give the parametric equations of the general solution to the homogenous equation \(\mathsf{A} \mathsf{x} = {\bf 0}\).
Describe the geometric form of your answer to part (a). For example, you answer should be something like: “it is a plane in \(\mathbb{R}^3\)” or “it is a line in \(\mathbb{R}^7\)” or “it is a point in \(\mathbb{R}^4\).”
Suppose that we also know that \(\mathsf{A}\begin{bmatrix} 4 \\ 1 \\ -3 \\ 2 \\ \end{bmatrix} = \begin{bmatrix} 22 \\ -13 \\ 7 \\ \end{bmatrix}\). Then give the general solution to \(\mathsf{A} \mathsf{x}= \begin{bmatrix} 22 \\ -13\\ 7 \\ \end{bmatrix}\) in parametric form.
2.3 RREF for a set of vectors
Suppose that we have five vectors \(\mathsf{v}_1, \mathsf{v}_2,\mathsf{v}_3,\mathsf{v}_4,\mathsf{v}_5\) in \(\mathbb{R}^4\) and that the matrix \[ A = \left[ \begin{array}{ccc} \mid & \mid & \mid & \mid & \mid \\ \mathsf{v}_1 & \mathsf{v}_2 & \mathsf{v}_3 &\mathsf{v}_4 &\mathsf{v}_5 \\ \mid & \mid & \mid & \mid & \mid \end{array} \right] \] has reduced row echelon form \[ \begin{bmatrix} 1 & 0 & -3 & 0 & 2 \\ 0 & 1 & 4 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}. \]
Do the vectors \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4, \mathsf{v}_5\) span \(\mathbb{R}^4\)? Justify your answer.
Is the vector \(\mathsf{v}_3\) in \(\mathrm{span}(\mathsf{v}_1,\mathsf{v}_2)\)? Justify your answer.
Pick any \(\mathsf{b}\) in \(\mathrm{span}(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4, \mathsf{v}_5)\). Is there always a unique way to write \(\mathsf{b}\) as a linear combination of \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4, \mathsf{v}_5\)? Justify your answer.
2.4 Removing free variable columns from a matrix
Consider the matrix
\[ A =\left[ \begin{array}{cccccc} 6 & 5 & -3 & 4 & 2 & -9 \\ -7 & -6 & 4 & -5 & -7 & 16 \\ -4 & -3 & -1 & 0 & -8 & 9 \\ 8 & 7 & -5 & 6 & 1 & -12 \end{array} \right]. \]
- Use RStudio to show that the columns of \(\mathsf{A}\) span \(\mathbb{R}^4\). You don’t need to turn in an R file here, just report the reduced row echelon form that you get.
- Write down the new matrix \(\mathsf{A}'\) gotten by removing the free variable columns from \(\mathsf{A}\).
- Without using additional calculations on RStudio, explain why the new system \(\mathsf{A}' \mathsf{x} = \mathsf{b}\) is consistent and has a unique solution for every choice of \(\mathsf{b} \in \mathbb{R}^4\).
2.5 A square matrix
Suppose that \(A\) is a \(5\times 5\) matrix and \(\mathsf{b}\) is a vector in \(\mathbb{R}^5\) with the property that \(A\mathsf{x}=\mathsf{b}\) has a unique solution. Explain why the columns of \(A\) must span \(\mathbb{R}^5\). Use the reduced row echelon form of \(A\) in your explanation.
2.6 Combining solutions to \(A \mathsf{x} = \mathsf{b}\)
Suppose that \(\mathsf{x}_1\) and \(\mathsf{x}_2\) are solutions to \(\mathsf{A} \mathsf{x} = \mathsf{b}\) (where \(\mathsf{b} \not= \mathsf{0}\)).
- Decide if any of the following are also solutions to \(\mathsf{A} \mathsf{x} = \mathsf{b}\).
- \(\mathsf{x}_1+ \mathsf{x}_2\)
- \(\mathsf{x}_1 - \mathsf{x}_2\)
- \(\frac{1}{2} ( \mathsf{x}_1 + \mathsf{x}_2)\)
- \(\frac{5}{2} \mathsf{x}_1 - \frac{3}{2} \mathsf{x}_2\).
- Under what conditions on \(c\) and \(d\) is \(\mathsf{x} = c \mathsf{x}_1 + d \mathsf{x}_2\) a solution to \(\mathsf{A} \mathsf{x} = \mathsf{b}\)? Justify your answer.
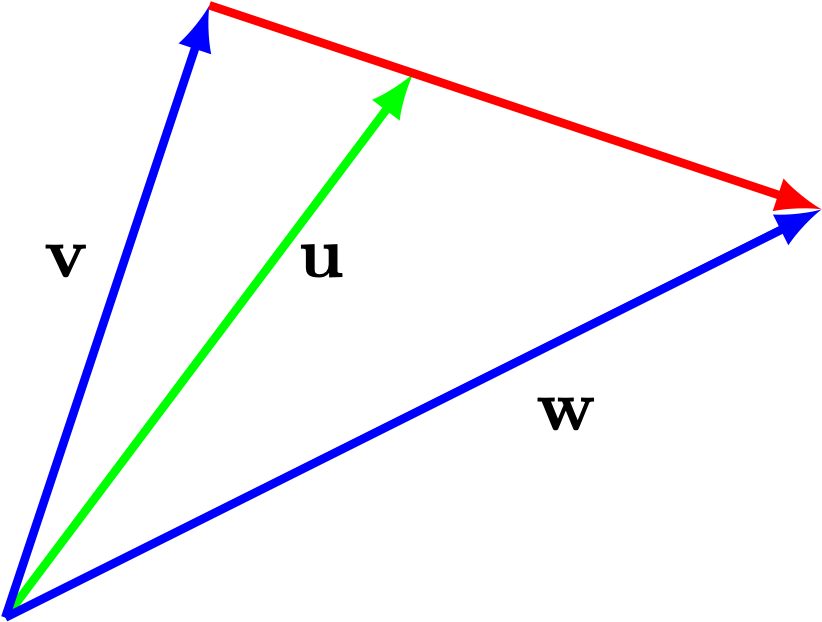
- Let \(\mathsf{u}\) be the vector that points to \(1/3\) of the way from the tip of \(\mathsf{v}\) to the tip of \(\mathsf{w}\) as depicted below.
- Write \(\mathsf{u}\) as a linear combination of \(\mathsf{v}\) and \(\mathsf{w}\) (hint: think about \(\mathsf{w} - \mathsf{v}\))
- If \(\mathsf{v}\) and \(\mathsf{w}\) are solutions to \(A x = \mathsf{b}\) then show that \(\mathsf{u}\) is also a solution to \(A \mathsf{x} = \mathsf{b}\).
2.7 A Balanced Diet
An athlete wants to consume a daily diet of 200 grams of carbohydrates, 60 grams of fats and 160 grams of proteins. Here are some of their favorite foods.
| food | carbs | fats | proteins |
|---|---|---|---|
| almonds | 3 | 8 | 5 |
| avocado | 15 | 31 | 4 |
| beans | 20 | 1 | 8 |
| bread | 12 | 1 | 2 |
| cheese | 1 | 5 | 3 |
| chicken | 0 | 13 | 50 |
| egg | 1 | 5 | 6 |
| milk | 12 | 8 | 8 |
| zucchini | 6 | 0 | 2 |
Answer the following questions, using RStudio for your calculations. Each response must use two or more of the following terms: linear combination, span, linearly dependent, linearly independent.
Explain why they cannot achieve their daily goal by eating only almonds, milk and zucchini.
Explain why they cannot achieve their daily goal by eating only almonds, beans and cheese.
Find a valid one-day diet consisting of almonds, chicken, and zucchini.
2.8 Missing Column
The matrices below are supposed to be \(3 \times 3\) but in each case the third column was accdentally deleted. In each case, add a third column, that has no 0s in it and is different from either the first or second column, so that the columns of \(A\) are linearly dependent and so that the columns of \(B\) are linearly independent. Briefly describe your strategy. \[ A=\left[ \begin{matrix} 1& 0 & \quad \\ 0& 1& \quad \\ 2& 2& \quad \\ \end{matrix}\right] \qquad\qquad B=\left[ \begin{matrix} 1& 0 & \quad \\ 0& 1& \quad \\ 2& 2& \quad \\ \end{matrix}\right] \]
2.9 Linear System
Use R to solve this problem. Do your computations in an R markdown file. Knit the file to HTML and include it with your homework. Here you can download a template for doing this problem (including the matrix typed out for you!). \[ A =\left[ \begin{array}{cccccc} 12 & 10 & -6 & 8 & 4 & -18 \\ -7 & -6 & 4 & -5 & -7 & 16 \\ 9 & 9 & -9 & 9 & 9 & -27 \\ -4 & -3 & -1 & 0 & -8 & 9 \\ 8 & 7 & -5 & 6 & 1 & -12 \\ \end{array} \right] \quad b = \begin{bmatrix} 14 \\ -12 \\ 9\\ -15 \\6 \end{bmatrix} \]
Show that the columns of \(A\) are linearly dependent by finding two different dependency relations among them. You can write your answer in a form like \(5 a1+ 4 a2 + 3 a3 + 2 a4 + a5 = 0\), where \(a1, a2,\) etc are the columns of \(A\).
Augment \(A\) with \(b\) and show that \(A x = b\) is consistent and has infinitely many solutions.
Remove the free-variable columns from \(A\) to get a new, smaller matrix \(A'\). Show that \(A' x = b\) has a unique solution and say what that solution is.